Mathématiques > Géométrie > Géométrie Analytique > Intersection de droites et de cercles

Intersection de Droites et de Cercles : Guide Complet

Comprendre et maîtriser le calcul des points d'intersection entre une droite et un cercle. Explications détaillées, exemples concrets et exercices corrigés pour les lycéens.

Introduction

Dans le domaine de la géométrie analytique, l'étude de l'intersection entre une droite et un cercle est un problème classique mais fondamental. Comprendre comment trouver les points où une droite et un cercle se croisent est essentiel pour résoudre de nombreux problèmes en mathématiques, en physique et en ingénierie. Ce guide vous fournira une explication détaillée et accessible, étape par étape, pour maîtriser ce concept.

Équations Fondamentales

Pour commencer, rappelons les équations fondamentales dont nous aurons besoin :

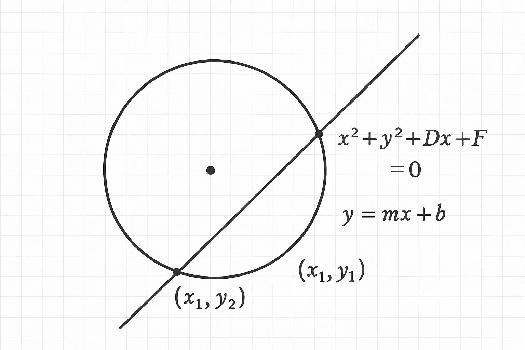
  • Équation d'un cercle : (x - a)² + (y - b)² = r², où (a, b) est le centre du cercle et r son rayon.
  • Équation d'une droite : y = mx + p, où m est la pente de la droite et p son ordonnée à l'origine. Nous pourrons également rencontrer la forme ax + by + c = 0.

Méthode de Résolution

La méthode générale pour trouver l'intersection entre une droite et un cercle consiste à résoudre un système d'équations :

  1. Substitution : Exprimez y en fonction de x (ou x en fonction de y) à partir de l'équation de la droite (y = mx + p).
  2. Remplacement : Remplacez cette expression dans l'équation du cercle : (x - a)² + (mx + p - b)² = r².
  3. Développement et Simplification : Développez et simplifiez l'équation résultante. Vous obtiendrez une équation du second degré en x (ou en y).
  4. Résolution de l'Équation du Second Degré : Résolvez cette équation du second degré. Rappelez-vous que :
    • Si le discriminant (Δ) est positif, il y a deux solutions (deux points d'intersection).
    • Si le discriminant est nul, il y a une solution (la droite est tangente au cercle).
    • Si le discriminant est négatif, il n'y a aucune solution (la droite ne croise pas le cercle).
  5. Calcul des Coordonnées : Pour chaque solution x (ou y), remplacez cette valeur dans l'équation de la droite (y = mx + p) pour trouver la coordonnée y (ou x) correspondante.

Exemple Concret

Considérons un cercle d'équation x² + y² = 25 (centre (0, 0), rayon 5) et une droite d'équation y = x + 1.

  1. Substitution : y = x + 1
  2. Remplacement : x² + (x + 1)² = 25
  3. Développement et Simplification : x² + x² + 2x + 1 = 25 => 2x² + 2x - 24 = 0 => x² + x - 12 = 0
  4. Résolution de l'Équation du Second Degré : Δ = 1² - 4(1)(-12) = 49. Les solutions sont x₁ = (-1 + √49) / 2 = 3 et x₂ = (-1 - √49) / 2 = -4.
  5. Calcul des Coordonnées : Pour x₁ = 3, y₁ = 3 + 1 = 4. Pour x₂ = -4, y₂ = -4 + 1 = -3.

Les points d'intersection sont donc (3, 4) et (-4, -3).

Cas Particuliers et Difficultés

Il est important de noter certains cas particuliers :

  • Droite Verticale : Si la droite est verticale (équation x = k), la méthode est similaire. Remplacez x par k dans l'équation du cercle.
  • Centre du Cercle non à l'Origine : Si le centre du cercle n'est pas à l'origine, utilisez l'équation générale (x - a)² + (y - b)² = r².
  • Équation de la Droite sous Forme Implicite : Si l'équation de la droite est donnée sous la forme ax + by + c = 0, il faut d'abord exprimer y en fonction de x (ou x en fonction de y) avant de substituer.

Les erreurs courantes incluent des erreurs de calcul lors du développement et de la simplification de l'équation, ou une mauvaise interprétation du discriminant.

Exercices

Exercice 1: Déterminez les points d'intersection du cercle (x-1)² + (y+2)² = 9 et de la droite y = x - 1.

Exercice 2: Trouvez l'équation de la tangente au cercle x² + y² = 4 au point (√2, √2).

Ce qu'il faut retenir

  • L'intersection d'une droite et d'un cercle se trouve en résolvant un système d'équations.
  • Substituez l'équation de la droite dans celle du cercle.
  • Résolvez l'équation du second degré obtenue. Le discriminant indique le nombre de points d'intersection.
  • Remplacez les valeurs de x (ou y) trouvées dans l'équation de la droite pour obtenir les coordonnées complètes des points d'intersection.
  • Soyez attentif aux cas particuliers comme les droites verticales et les cercles dont le centre n'est pas à l'origine.

← Fonctions Trigonométriques Réciproques dans le Triangle Rectangle Intersection de droites et de plans dans l'espace →

FAQ

  • Comment savoir si une droite est tangente à un cercle ?

    Une droite est tangente à un cercle si l'équation du second degré obtenue après substitution a un discriminant nul (Δ = 0). Cela signifie qu'il y a une seule solution, donc un seul point d'intersection.
  • Que faire si je trouve un discriminant négatif ?

    Si le discriminant est négatif, cela signifie que l'équation du second degré n'a pas de solutions réelles. Par conséquent, la droite et le cercle ne se coupent pas.
  • Est-ce que cette méthode fonctionne pour tous les cercles et toutes les droites ?

    Oui, cette méthode fonctionne pour tous les cercles et toutes les droites, quelle que soit leur équation. Il faut simplement adapter la substitution et faire attention aux cas particuliers (droite verticale, cercle dont le centre n'est pas à l'origine).