Mathématiques > Algèbre > Fonctions > Représentation graphique d'une fonction

Introduction à la Représentation Graphique des Fonctions

Apprenez à représenter graphiquement une fonction, étape par étape. Ce guide complet vous explique comment tracer des graphiques de fonctions linéaires, quadratiques, et plus encore, avec des exemples détaillés et des conseils pratiques pour réussir vos exercices.

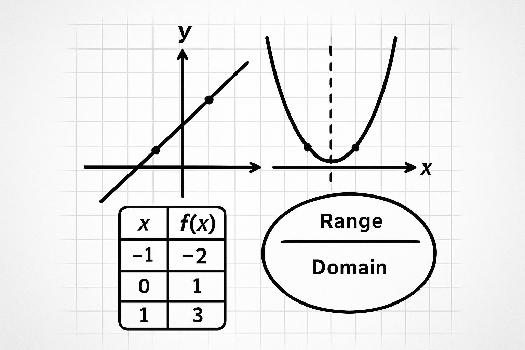
Qu'est-ce qu'une Représentation Graphique d'une Fonction?

La représentation graphique d'une fonction est un dessin qui illustre la relation entre les entrées (les valeurs de x) et les sorties (les valeurs de y ou f(x)). Chaque point sur le graphique correspond à une paire (x, y) qui satisfait l'équation de la fonction.

En d'autres termes, c'est une manière visuelle de comprendre comment la valeur de f(x) change lorsque x varie.

Fonctions Linéaires

Une fonction linéaire a la forme f(x) = mx + b, où m est la pente et b est l'ordonnée à l'origine. Sa représentation graphique est une droite.

Exemple: Soit la fonction f(x) = 2x + 1.

  • Pente: m = 2 (pour chaque augmentation de 1 unité de x, y augmente de 2 unités).
  • Ordonnée à l'origine: b = 1 (le point où la droite coupe l'axe des y est (0, 1)).

Pour tracer la droite, trouvez deux points sur la droite (par exemple, en substituant x = 0 et x = 1 dans l'équation) et tracez une droite passant par ces deux points.

Fonctions Quadratiques

Une fonction quadratique a la forme f(x) = ax2 + bx + c, où a, b, et c sont des constantes et a ≠ 0. Sa représentation graphique est une parabole.

Points clés pour tracer une parabole:

  • Sommet: Le point le plus bas (si a > 0) ou le plus haut (si a < 0) de la parabole. Les coordonnées du sommet sont données par (-b/2a, f(-b/2a)).
  • Axe de symétrie: Une droite verticale passant par le sommet. Son équation est x = -b/2a.
  • Racines (zéros): Les points où la parabole coupe l'axe des x (c'est-à-dire, les valeurs de x pour lesquelles f(x) = 0). Vous pouvez les trouver en résolvant l'équation quadratique ax2 + bx + c = 0.
  • Ordonnée à l'origine: Le point où la parabole coupe l'axe des y (c'est-à-dire, f(0) = c).

Exemple: Soit la fonction f(x) = x2 - 4x + 3.

  • Sommet: x = -(-4)/(2*1) = 2, f(2) = 22 - 4*2 + 3 = -1. Le sommet est (2, -1).
  • Axe de symétrie: x = 2.
  • Racines: En résolvant x2 - 4x + 3 = 0, on trouve x = 1 et x = 3. Les racines sont (1, 0) et (3, 0).
  • Ordonnée à l'origine: f(0) = 3. Le point est (0, 3).

En utilisant ces points, vous pouvez tracer la parabole.

Fonctions Cubiques

Une fonction cubique a la forme f(x) = ax3 + bx2 + cx + d. La représentation graphique est une courbe plus complexe. Identifier les points clés est essentiel.

Points clés à considérer:

  • Zéros/Racines: Les points où la courbe coupe l'axe des x. Résoudre l'équation f(x) = 0 peut être complexe, mais peut être simplifié si on peut factoriser l'expression.
  • Points d'inflexion: Les points où la courbure de la fonction change. Trouver ces points nécessite l'utilisation de la dérivée seconde (concept du niveau supérieur au lycée, mais on peut souvent les deviner en regardant l'allure générale).
  • Comportement aux infinis: Regarder comment la fonction se comporte lorsque x tend vers +∞ et -∞. Ceci est dominé par le terme de plus haut degré (ici ax3). Si a est positif, f(x) tend vers +∞ quand x tend vers +∞ et vers -∞ quand x tend vers -∞. Si a est négatif, c'est l'inverse.

Exemple: Soit la fonction f(x) = x3 - 3x

  • Zéros: x3 - 3x = x(x2 - 3) = 0, donc x = 0, x = √3, x = -√3.
  • Comportement aux infinis: Comme le coefficient de x3 est positif, la fonction tend vers +∞ lorsque x tend vers +∞ et vers -∞ lorsque x tend vers -∞.

Tracer des points additionnels entre les zéros peut aider à affiner le tracé de la courbe.

Tableau de Valeurs

Un tableau de valeurs est un outil essentiel pour tracer le graphique d'une fonction. Il consiste à choisir plusieurs valeurs de x, à calculer les valeurs correspondantes de f(x), et à reporter ces paires (x, f(x)) dans un tableau.

Exemple: Pour la fonction f(x) = x2 - 2x + 1:

x f(x)
-1 4
0 1
1 0
2 1
3 4

Ensuite, tracez ces points sur un plan cartésien et reliez-les pour obtenir la courbe de la fonction.

Domaine et Image

Domaine: L'ensemble de toutes les valeurs possibles de x pour lesquelles la fonction est définie.

Image: L'ensemble de toutes les valeurs possibles de f(x) que la fonction peut prendre.

Comprendre le domaine et l'image d'une fonction peut vous aider à identifier les limites de son graphique et à éviter les erreurs lors du tracé.

Ce qu'il faut retenir

  • La représentation graphique d'une fonction est un dessin qui illustre la relation entre les entrées (x) et les sorties (f(x)).
  • Les fonctions linéaires ont une représentation graphique en forme de droite.
  • Les fonctions quadratiques ont une représentation graphique en forme de parabole. Il est important de déterminer le sommet, l'axe de symétrie, les racines et l'ordonnée à l'origine.
  • Un tableau de valeurs est un outil utile pour tracer le graphique d'une fonction.
  • Le domaine est l'ensemble des valeurs possibles de x, et l'image est l'ensemble des valeurs possibles de f(x).

← Introduction intuitive à la continuité d'une fonction Inéquations avec Valeurs Absolues : Guide Complet pour le Lycée →

FAQ

  • Comment puis-je vérifier si mon graphique est correct?

    Vérifiez si tous les points que vous avez calculés à partir de l'équation de la fonction se trouvent bien sur le graphique. Utilisez un logiciel de traçage de graphes pour comparer votre résultat.
  • Que faire si je ne peux pas trouver les racines d'une fonction quadratique facilement?

    Utilisez la formule quadratique pour trouver les racines. Si le discriminant est négatif, cela signifie que la fonction n'a pas de racines réelles et que la parabole ne coupe pas l'axe des x.
  • Qu'est-ce que l'ordonnée à l'origine et comment la trouver?

    L'ordonnée à l'origine est le point où le graphique de la fonction coupe l'axe des y. Pour la trouver, il suffit de calculer f(0).