Mathématiques > Algèbre > Équations et Inéquations > Résolution graphique d'équations et d'inéquations
Résolution graphique d'équations et d'inéquations : Une approche visuelle
Apprenez à résoudre des équations et des inéquations grâce à leurs représentations graphiques. Cette méthode offre une compréhension intuitive des solutions et complète les techniques algébriques.
Introduction à la résolution graphique
La résolution graphique d'équations et d'inéquations consiste à trouver les solutions en analysant les graphiques des fonctions associées. Cette approche est particulièrement utile pour visualiser les solutions et comprendre leur nature.
Avantages de la méthode graphique :
- Intuition visuelle : Facilite la compréhension des solutions.
- Solutions approximatives : Permet d'estimer les solutions même lorsque les méthodes algébriques sont complexes.
- Visualisation des ensembles de solutions : Idéale pour les inéquations, où les solutions sont souvent des intervalles.
Résolution graphique d'une équation f(x) = 0
Pour résoudre graphiquement une équation de la forme f(x) = 0, on trace la courbe représentative de la fonction f(x). Les solutions de l'équation sont les abscisses des points où la courbe coupe l'axe des abscisses (axe des x). Ces points sont appelés zéros ou racines de la fonction.
Exemple : Soit l'équation x² - 4 = 0. On trace la courbe de la fonction f(x) = x² - 4. La courbe coupe l'axe des abscisses aux points d'abscisses -2 et 2. Donc, les solutions de l'équation sont x = -2 et x = 2.
Important : L'échelle du graphique est cruciale pour une lecture précise des solutions. Utiliser un logiciel de traçage de courbes ou une calculatrice graphique facilite grandement le processus.
Résolution graphique d'une équation f(x) = g(x)
Pour résoudre graphiquement une équation de la forme f(x) = g(x), on trace les courbes représentatives des fonctions f(x) et g(x) sur le même graphique. Les solutions de l'équation sont les abscisses des points où les deux courbes se coupent.
Exemple : Soit l'équation x + 1 = x² - 1. On trace la courbe de f(x) = x + 1 (une droite) et la courbe de g(x) = x² - 1 (une parabole). Les points d'intersection des deux courbes ont pour abscisses -1 et 2. Donc, les solutions de l'équation sont x = -1 et x = 2.
Cas particulier : Si les courbes ne se coupent pas, l'équation n'a pas de solution réelle.
Résolution graphique d'une inéquation f(x) > 0 (ou f(x) < 0)
Pour résoudre graphiquement une inéquation de la forme f(x) > 0, on trace la courbe représentative de la fonction f(x). Les solutions de l'inéquation sont les intervalles des abscisses pour lesquels la courbe est située au-dessus de l'axe des abscisses.
De même, pour résoudre f(x) < 0, on cherche les intervalles où la courbe est située en dessous de l'axe des abscisses.
Exemple : Soit l'inéquation x² - 4 > 0. On trace la courbe de f(x) = x² - 4. La courbe est au-dessus de l'axe des abscisses pour x < -2 et pour x > 2. Donc, la solution de l'inéquation est x ∈ ]-∞, -2[ ∪ ]2, +∞[.
Attention : Il faut exclure les points où la courbe coupe l'axe des abscisses si l'inéquation est stricte (> ou <). Si l'inéquation est large (≥ ou ≤), on inclut ces points.
Résolution graphique d'une inéquation f(x) > g(x) (ou f(x) < g(x))
Pour résoudre graphiquement une inéquation de la forme f(x) > g(x), on trace les courbes représentatives des fonctions f(x) et g(x) sur le même graphique. Les solutions de l'inéquation sont les intervalles des abscisses pour lesquels la courbe de f(x) est située au-dessus de la courbe de g(x).
De même, pour résoudre f(x) < g(x), on cherche les intervalles où la courbe de f(x) est située en dessous de la courbe de g(x).
Exemple : Soit l'inéquation x + 1 > x² - 1. On trace les courbes de f(x) = x + 1 et g(x) = x² - 1. La droite est au-dessus de la parabole pour -1 < x < 2. Donc, la solution de l'inéquation est x ∈ ]-1, 2[.
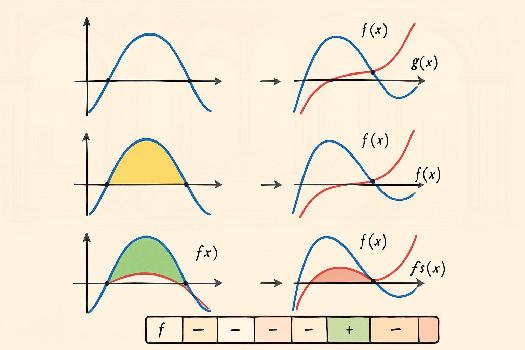
Tableau de signes et résolution graphique
Le tableau de signes est un outil puissant qui complète la résolution graphique d'inéquations. Il permet d'organiser l'information sur le signe de f(x) sur différents intervalles et de visualiser rapidement les solutions d'inéquations telles que f(x) > 0 ou f(x) < 0.
Création d'un tableau de signes :
- Identifier les racines de f(x) : Trouvez les valeurs de x pour lesquelles f(x) = 0. Ces valeurs correspondent aux abscisses des points où le graphe de f(x) croise l'axe des x.
- Identifier les points de discontinuité (si applicable) : Pour les fonctions rationnelles ou définies par morceaux, identifiez les valeurs de x où la fonction n'est pas définie.
- Créer le tableau : Construisez un tableau avec une ligne pour x (allant de -∞ à +∞), une ligne pour chaque facteur de f(x) (si f(x) est factorisable) et une ligne pour f(x).
- Remplir le tableau : Pour chaque facteur et pour f(x), indiquez le signe (+ ou -) sur chaque intervalle délimité par les racines et les points de discontinuité. N'oubliez pas d'indiquer les racines (0) et les valeurs interdites (||) dans le tableau.
Interprétation du tableau de signes :
- f(x) > 0 : Les intervalles où la ligne de f(x) est positive (+) correspondent aux solutions de l'inéquation f(x) > 0. Sur le graphique, cela correspond aux portions de la courbe qui sont au-dessus de l'axe des x.
- f(x) < 0 : Les intervalles où la ligne de f(x) est négative (-) correspondent aux solutions de l'inéquation f(x) < 0. Sur le graphique, cela correspond aux portions de la courbe qui sont en dessous de l'axe des x.
Exemple :
Considérons la fonction f(x) = (x - 1)(x + 2). Les racines sont x = 1 et x = -2.
Tableau de signes :
| x | -∞ | -2 | 1 | +∞ | ||
|---|---|---|---|---|---|---|
| x - 1 | - | - | - | 0 | + | + |
| x + 2 | - | 0 | + | + | + | + |
| f(x) | + | 0 | - | 0 | + | + |
Résolution graphique :
Si vous tracez le graphe de f(x) = (x - 1)(x + 2), vous verrez que :
- La courbe est au-dessus de l'axe des x pour x < -2 et x > 1. Ceci correspond à f(x) > 0.
- La courbe est en dessous de l'axe des x pour -2 < x < 1. Ceci correspond à f(x) < 0.
Le tableau de signes confirme donc les solutions que l'on peut lire sur le graphe.
Conclusion :
La combinaison de la résolution graphique et du tableau de signes est une méthode puissante pour résoudre les inéquations. La représentation graphique offre une visualisation intuitive, tandis que le tableau de signes permet une analyse plus rigoureuse et précise des solutions.
Ce qu'il faut retenir
- Équation f(x) = 0 : Les solutions sont les abscisses des points d'intersection de la courbe de f(x) avec l'axe des abscisses.
- Équation f(x) = g(x) : Les solutions sont les abscisses des points d'intersection des courbes de f(x) et g(x).
- Inéquation f(x) > 0 : Les solutions sont les intervalles où la courbe de f(x) est au-dessus de l'axe des abscisses.
- Inéquation f(x) < 0 : Les solutions sont les intervalles où la courbe de f(x) est en dessous de l'axe des abscisses.
- Inéquation f(x) > g(x) : Les solutions sont les intervalles où la courbe de f(x) est au-dessus de la courbe de g(x).
- Inéquation f(x) < g(x) : Les solutions sont les intervalles où la courbe de f(x) est en dessous de la courbe de g(x).
- Le tableau de signes: est un outil permettant d'organiser et de visualiser le signe d'une fonction sur différents intervalles. Combiné à la résolution graphique, il offre une méthode complète et rigoureuse pour résoudre les inéquations.
FAQ
-
Est-ce que la méthode graphique est toujours précise ?
La précision de la méthode graphique dépend de l'échelle du graphique et de la précision de sa construction. Elle est souvent suffisante pour obtenir une approximation des solutions, mais peut être moins précise que les méthodes algébriques. -
Que faire si la courbe ne coupe pas l'axe des abscisses ?
Si la courbe de f(x) ne coupe pas l'axe des abscisses, cela signifie que l'équation f(x) = 0 n'a pas de solution réelle. -
Peut-on utiliser une calculatrice graphique pour résoudre des équations et des inéquations graphiquement ?
Oui, les calculatrices graphiques sont un outil très pratique pour tracer les courbes des fonctions et identifier leurs points d'intersection avec l'axe des abscisses ou avec d'autres courbes.
