Mathématiques > Algèbre > Fonctions > Fonctions affines

Fonctions Affines : Guide Complet et Exemples

Découvrez tout ce que vous devez savoir sur les fonctions affines : définition, propriétés, représentation graphique, et applications. Un cours complet avec exemples et exercices pour le lycée.

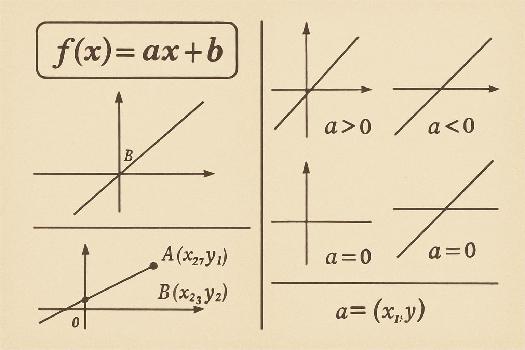
Définition et Forme Générale

La fonction affine est un concept fondamental en algèbre. Elle représente une relation linéaire entre deux variables. Définition : Une fonction f est dite affine si elle peut s'écrire sous la forme f(x) = ax + b, où a et b sont des nombres réels.

  • a est le coefficient directeur (ou pente) : Il indique la variation de f(x) pour chaque unité de variation de x. Un a positif signifie une fonction croissante, un a négatif une fonction décroissante, et a nul une fonction constante.
  • b est l'ordonnée à l'origine : C'est la valeur de f(x) lorsque x = 0. Graphiquement, c'est le point où la droite représentant la fonction coupe l'axe des ordonnées.

Exemple : f(x) = 2x + 3 est une fonction affine où a = 2 et b = 3.

Représentation Graphique

La représentation graphique d'une fonction affine est une droite. Pour tracer cette droite, il suffit de connaître deux points.

Méthode :

  1. Choisissez deux valeurs de x (par exemple, x = 0 et x = 1).
  2. Calculez les valeurs correspondantes de f(x).
  3. Placez les deux points obtenus dans un repère.
  4. Tracez la droite passant par ces deux points.

Exemple : Pour f(x) = 2x + 3 :
  • Si x = 0, alors f(0) = 2*0 + 3 = 3. Point (0, 3).
  • Si x = 1, alors f(1) = 2*1 + 3 = 5. Point (1, 5).
Tracez la droite passant par (0, 3) et (1, 5).

Note : Une fonction linéaire est un cas particulier de fonction affine où b = 0. Sa représentation graphique passe toujours par l'origine (0, 0).

Détermination de l'Équation d'une Fonction Affine

Il existe plusieurs méthodes pour déterminer l'équation d'une fonction affine (trouver a et b) :

1. À partir de deux points :
Si on connaît deux points de la droite, par exemple (x1, y1) et (x2, y2), on peut calculer le coefficient directeur a comme suit :

a = (y2 - y1) / (x2 - x1)

Une fois a trouvé, on peut utiliser l'un des deux points pour trouver b en remplaçant x et f(x) dans l'équation f(x) = ax + b.

Exemple : Soit les points (1, 5) et (2, 7).
a = (7 - 5) / (2 - 1) = 2.
En utilisant le point (1, 5) : 5 = 2*1 + b, donc b = 3.
L'équation de la fonction affine est donc f(x) = 2x + 3.

2. À partir du coefficient directeur et d'un point :
Si on connaît le coefficient directeur a et un point (x0, y0), on peut directement remplacer a, x et f(x) dans l'équation f(x) = ax + b pour trouver b.

Exemple : Si a = -1 et la droite passe par (0, 4).
4 = -1*0 + b, donc b = 4.
L'équation de la fonction affine est f(x) = -x + 4.

Sens de Variation

Le signe du coefficient directeur a détermine le sens de variation de la fonction affine :

  • Si a > 0, la fonction est croissante. Quand x augmente, f(x) augmente aussi.
  • Si a < 0, la fonction est décroissante. Quand x augmente, f(x) diminue.
  • Si a = 0, la fonction est constante. f(x) est toujours égale à b, quelle que soit la valeur de x. La droite est horizontale.

Exemple :
  • f(x) = 3x + 1 est croissante car a = 3 > 0.
  • f(x) = -2x + 5 est décroissante car a = -2 < 0.
  • f(x) = 4 est constante car a = 0.

Applications des Fonctions Affines

Les fonctions affines ont de nombreuses applications dans la vie réelle, notamment en physique, en économie et en statistique.

Exemples :

  • Calcul d'un coût : Le coût total d'un service peut être une fonction affine du nombre d'unités utilisées (par exemple, le coût d'une course en taxi en fonction de la distance parcourue).
  • Conversion d'unités : La conversion de Celsius en Fahrenheit est une fonction affine (F = (9/5)C + 32).
  • Modélisation linéaire : Les fonctions affines peuvent être utilisées pour modéliser des relations linéaires entre deux variables dans des données statistiques.

Exercice : Un taxi facture une prise en charge de 2€ et 0.50€ par kilomètre. Exprimez le coût total de la course en fonction du nombre de kilomètres parcourus. Quelle est la fonction affine qui représente cette situation ?
Réponse : f(x) = 0.5x + 2

Ce qu'il faut retenir

  • Une fonction affine est de la forme f(x) = ax + b, où a est le coefficient directeur et b l'ordonnée à l'origine.
  • La représentation graphique d'une fonction affine est une droite.
  • Le coefficient directeur a détermine le sens de variation de la fonction : croissante si a > 0, décroissante si a < 0, constante si a = 0.
  • On peut déterminer l'équation d'une fonction affine à partir de deux points, ou à partir du coefficient directeur et d'un point.
  • Les fonctions affines ont de nombreuses applications pratiques.

← Factorisation et racines des polynômes : Techniques et applications Fonctions Linéaires et Proportionnalité →

FAQ

  • Comment identifier une fonction affine ?

    Une fonction est affine si elle peut s'écrire sous la forme f(x) = ax + b, où a et b sont des nombres réels. Si vous pouvez exprimer la relation entre x et f(x) sous cette forme, alors c'est une fonction affine.
  • Quelle est la différence entre une fonction affine et une fonction linéaire ?

    Une fonction linéaire est un cas particulier d'une fonction affine où b = 0. Donc, une fonction linéaire s'écrit f(x) = ax et sa représentation graphique passe par l'origine (0, 0).
  • Comment tracer rapidement la droite représentant une fonction affine ?

    Il suffit de calculer les coordonnées de deux points. Choisissez deux valeurs simples pour x (par exemple, 0 et 1), calculez les valeurs correspondantes de f(x), placez ces deux points dans un repère, et tracez la droite qui les relie.