Mathématiques > Logique et Raisonnement Mathématique > Types de Raisonnement > Raisonnement par induction

Le Raisonnement par Induction : Un Guide Complet

Explorez le raisonnement par induction, une méthode puissante pour prouver des propositions mathématiques valables pour tous les nombres naturels. Apprenez les étapes clés et visualisez des exemples concrets pour maîtriser cette technique essentielle au lycée.

Introduction au Raisonnement par Induction

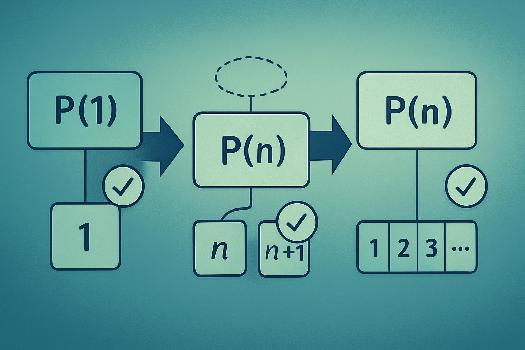
Le raisonnement par induction (ou récurrence) est une technique de preuve mathématique utilisée pour démontrer qu'une proposition P(n) est vraie pour tous les nombres naturels n (ou pour tous les nombres naturels à partir d'un certain rang). C'est un outil fondamental en mathématiques, notamment en arithmétique, en algèbre et en analyse. L'idée principale est de montrer que si la proposition est vraie pour un certain nombre, elle est aussi vraie pour le nombre suivant. C'est un peu comme un effet domino : si on fait tomber le premier domino et que chaque domino qui tombe fait tomber le suivant, alors tous les dominos tomberont.

Les Étapes Clés du Raisonnement par Induction

Le raisonnement par induction se déroule en trois étapes principales :

  1. Initialisation : On montre que la proposition P(n) est vraie pour le premier nombre naturel, généralement n = 0 ou n = 1. C'est le premier domino qui tombe.
  2. Hérédité : On suppose que la proposition P(n) est vraie pour un nombre naturel quelconque n. Cette supposition est appelée l'hypothèse de récurrence. On doit alors démontrer que la proposition P(n+1) est également vraie. C'est montrer que si un domino tombe, le suivant tombera aussi.
  3. Conclusion : Si les étapes d'initialisation et d'hérédité sont vérifiées, alors on peut conclure que la proposition P(n) est vraie pour tous les nombres naturels n (à partir du rang initial).
Il est crucial de bien comprendre que l'étape d'hérédité ne consiste pas à prouver que P(n) est vraie. On suppose que P(n) est vraie et on utilise cette supposition pour démontrer que P(n+1) est vraie.

Exemple 1 : Somme des n premiers entiers

Démontrons par induction que la somme des n premiers entiers naturels est égale à n(n+1)/2, c'est-à-dire que : P(n) : 1 + 2 + 3 + ... + n = n(n+1)/2 1. Initialisation : Pour n = 1, on a P(1) : 1 = 1(1+1)/2 = 1. Donc P(1) est vraie. 2. Hérédité : Supposons que P(n) est vraie pour un certain n, c'est-à-dire que 1 + 2 + 3 + ... + n = n(n+1)/2 (hypothèse de récurrence). Montrons que P(n+1) est vraie, c'est-à-dire que 1 + 2 + 3 + ... + (n+1) = (n+1)(n+2)/2. On part de la somme des n+1 premiers entiers : 1 + 2 + 3 + ... + (n+1) = (1 + 2 + 3 + ... + n) + (n+1) En utilisant l'hypothèse de récurrence, on remplace la somme des n premiers entiers par n(n+1)/2 : = n(n+1)/2 + (n+1) = [n(n+1) + 2(n+1)]/2 = (n+1)(n+2)/2 On a bien montré que P(n+1) est vraie. 3. Conclusion : Puisque les étapes d'initialisation et d'hérédité sont vérifiées, on peut conclure que la somme des n premiers entiers naturels est égale à n(n+1)/2 pour tout nombre naturel n.

Exemple 2 : Divisibilité

Démontrons par induction que pour tout entier naturel n, 4n - 1 est divisible par 3. P(n) : 4n - 1 est divisible par 3 1. Initialisation : Pour n = 0, on a 40 - 1 = 1 - 1 = 0, et 0 est divisible par 3. Donc P(0) est vraie. 2. Hérédité : Supposons que P(n) est vraie pour un certain n, c'est-à-dire que 4n - 1 est divisible par 3 (hypothèse de récurrence). Cela signifie qu'il existe un entier k tel que 4n - 1 = 3k. Montrons que P(n+1) est vraie, c'est-à-dire que 4n+1 - 1 est divisible par 3. On part de 4n+1 - 1 : 4n+1 - 1 = 4 * 4n - 1 = 4 * 4n - 4 + 3 (on ajoute et soustrait 4 pour faire apparaître le terme 4n - 1) = 4(4n - 1) + 3 En utilisant l'hypothèse de récurrence, on remplace 4n - 1 par 3k : = 4(3k) + 3 = 3(4k + 1) Puisque 4k + 1 est un entier, 3(4k + 1) est divisible par 3. Donc 4n+1 - 1 est divisible par 3, et P(n+1) est vraie. 3. Conclusion : Puisque les étapes d'initialisation et d'hérédité sont vérifiées, on peut conclure que 4n - 1 est divisible par 3 pour tout nombre naturel n.

Quand utiliser le Raisonnement par Induction ?

Le raisonnement par induction est particulièrement utile pour prouver des propositions qui concernent des suites, des sommes, des inégalités, ou des propriétés de divisibilité impliquant des nombres naturels. C'est un outil puissant pour établir des vérités mathématiques générales à partir de cas particuliers.

Ce qu'il faut retenir

  • Le raisonnement par induction est une méthode de preuve pour démontrer des propositions vraies pour tous les entiers naturels.
  • Les trois étapes clés sont : Initialisation, Hérédité, et Conclusion.
  • L'Initialisation vérifie la proposition pour le premier entier.
  • L'Hérédité suppose que la proposition est vraie pour un entier n et démontre qu'elle est vraie pour l'entier suivant n+1.
  • La Conclusion affirme la validité de la proposition pour tous les entiers naturels à partir du rang initial.
  • L'hypothèse de récurrence est cruciale dans l'étape d'hérédité.

← Le Raisonnement par Déduction en Mathématiques Le Raisonnement par l'Absurde : Une Méthode Déductive Puissante →

FAQ

  • Quelle est la différence entre l'induction et la déduction ?

    La déduction part de principes généraux pour arriver à une conclusion spécifique (par exemple, tous les hommes sont mortels, Socrate est un homme, donc Socrate est mortel). L'induction, elle, part de cas spécifiques pour généraliser une propriété à tous les cas (par exemple, on observe que la somme des n premiers entiers semble toujours être n(n+1)/2, et on le démontre par induction pour le prouver pour tout n).
  • Que se passe-t-il si l'étape d'initialisation échoue ?

    Si l'étape d'initialisation échoue, la proposition n'est pas vraie pour tous les nombres naturels. Le raisonnement par induction ne peut donc pas être appliqué.
  • Que se passe-t-il si l'étape d'hérédité échoue ?

    Si l'étape d'hérédité échoue, cela signifie que même si la proposition est vraie pour un certain nombre, elle n'est pas nécessairement vraie pour le nombre suivant. Le raisonnement par induction ne peut donc pas être appliqué.