L'Algorithme de Dijkstra : Trouver le Plus Court Chemin

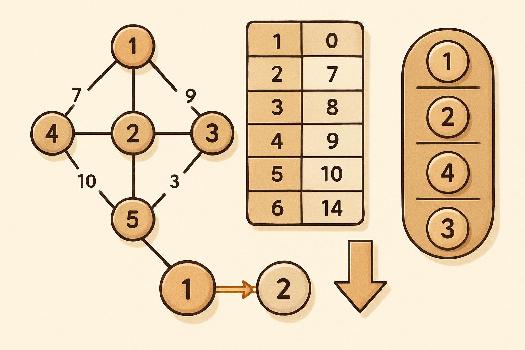
Introduction à l'Algorithme de Dijkstra

L'algorithme de Dijkstra est un algorithme fondamental en théorie des graphes. Son but est de trouver le chemin le plus court entre un sommet de départ et tous les autres sommets d'un graphe, ou jusqu'à un sommet d'arrivée spécifique. Il est largement utilisé dans des applications telles que la navigation GPS, le routage de réseaux et la planification de chemins. Il fonctionne uniquement sur des graphes avec des poids positifs.

Les Concepts Clés

Pour comprendre l'algorithme de Dijkstra, il est important de connaître les concepts suivants:

• Graphe pondéré: Un graphe où chaque arête a un poids (coût) associé.
• Sommet: Un nœud dans le graphe.
• Chemin: Une séquence de sommets connectés par des arêtes.
• Poids d'un chemin: La somme des poids des arêtes dans un chemin.
• Plus court chemin: Le chemin entre deux sommets avec le poids minimal.

Étapes de l'Algorithme de Dijkstra

L'algorithme de Dijkstra se déroule en plusieurs étapes:

1. Initialisation: Attribuer une distance de 0 au sommet de départ et une distance infinie (ou une valeur très grande) à tous les autres sommets. Créer un ensemble de sommets non visités.
2. Itération: Tant que l'ensemble des sommets non visités n'est pas vide:
   • Sélectionner le sommet non visité avec la distance minimale actuelle. Appelons ce sommet 'u'.
   • Marquer 'u' comme visité.
   • Pour chaque voisin 'v' de 'u':
     • Calculer la distance potentielle de la source à 'v' en passant par 'u' (distance[u] + poids(u, v)).
     • Si cette distance potentielle est inférieure à la distance actuelle de 'v', mettre à jour la distance de 'v' avec cette valeur.
3. Terminaison: L'algorithme se termine lorsque tous les sommets ont été visités ou lorsque le sommet d'arrivée a été atteint. Les distances obtenues représentent les longueurs des plus courts chemins depuis le sommet de départ.

Exemple Concret

Considérons un graphe avec les sommets A, B, C, D et E, et les poids suivants entre les arêtes:
A vers B: 4, A vers C: 2, B vers C: 1, B vers D: 5, C vers D: 8, C vers E: 10, D vers E: 2,
Nous voulons trouver le plus court chemin de A à E.

• Initialisation: A=0, B=∞, C=∞, D=∞, E=∞.
• Étape 1: On part de A (distance la plus courte actuelle). On regarde ses voisins: B (distance 4) et C (distance 2). On met à jour les distances de B et C.
• Étape 2: On choisit C (distance la plus courte actuelle parmi les non visités). Les voisins de C sont B (distance 2+1=3, on met à jour la distance de B car 3 < ∞), D (distance 2+8=10, on met à jour la distance de D), et E (distance 2+10=12, on met à jour la distance de E).
• Étape 3: On choisit B (distance la plus courte actuelle parmi les non visités). Le voisin de B est D (distance 3+5=8, on met à jour la distance de D car 8 < 10).
• Étape 4: On choisit D (distance la plus courte actuelle parmi les non visités). Le voisin de D est E (distance 8+2=10, on met à jour la distance de E car 10 < 12).
• Étape 5: Le seul sommet non visité est E. La distance de A à E est 10.

Pseudo-code

Voici le pseudo-code de l'algorithme de Dijkstra:

fonction Dijkstra(graphe, sommet_depart):
  distances = un tableau de distances de sommet_depart à tous les autres sommets
  prédécesseurs = un tableau de prédécesseurs pour reconstituer le chemin le plus court
  sommets_non_visités = un ensemble contenant tous les sommets du graphe

  pour chaque sommet dans graphe:
    distances[sommet] = infini  // Initialiser toutes les distances à l'infini
    prédécesseurs[sommet] = null // Initialiser tous les prédécesseurs à null

  distances[sommet_depart] = 0    // La distance de sommet_depart à lui-même est 0

  tant que sommets_non_visités n'est pas vide:
    sommet_courant = le sommet dans sommets_non_visités avec la distance minimale dans distances

    supprimer sommet_courant de sommets_non_visités

    pour chaque voisin de sommet_courant:
      nouvelle_distance = distances[sommet_courant] + poids(sommet_courant, voisin)

      si nouvelle_distance < distances[voisin]:
        distances[voisin] = nouvelle_distance
        prédécesseurs[voisin] = sommet_courant

  retourner distances, prédécesseurs

Implémentation

Pour implémenter l'algorithme de Dijkstra, on peut utiliser différentes structures de données comme les tableaux pour stocker les distances et les sommets visités, et les files de priorité (tas) pour optimiser la recherche du sommet avec la distance minimale. Le choix de la structure de données influence la complexité temporelle de l'algorithme.

Ce qu'il faut retenir

• L'algorithme de Dijkstra trouve le plus court chemin entre un sommet source et tous les autres sommets d'un graphe pondéré avec des poids positifs.
• Il utilise une approche itérative pour mettre à jour les distances estimées des sommets à partir de la source.
• Il maintient un ensemble de sommets non visités et sélectionne à chaque étape le sommet non visité avec la distance minimale.
• Les distances sont mises à jour en considérant les voisins du sommet courant.
• L'algorithme se termine lorsque tous les sommets ont été visités ou lorsque le sommet de destination a été atteint.
• Il est essentiel que les poids des arêtes soient positifs pour garantir le bon fonctionnement de l'algorithme.