Conjugué et Module d'un Nombre Complexe : Guide Complet

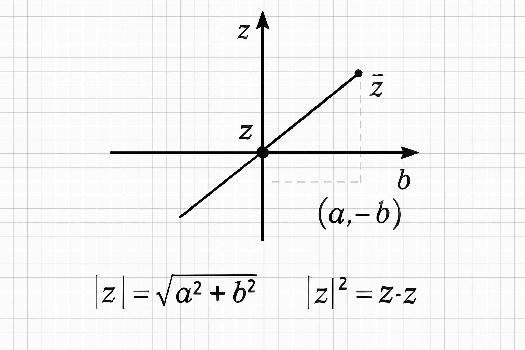
Définition du Conjugué d'un Nombre Complexe

Soit z = a + ib un nombre complexe, où a et b sont des nombres réels. Le conjugué de z, noté z̄ (lire 'z barre'), est défini par z̄ = a - ib. En d'autres termes, on change le signe de la partie imaginaire.

Exemples de Calcul de Conjugués

• Si z = 3 + 2i, alors z̄ = 3 - 2i.
• Si z = -1 - i, alors z̄ = -1 + i.
• Si z = 5 (un nombre réel), alors z̄ = 5.
• Si z = -4i (un imaginaire pur), alors z̄ = 4i.

Interprétation Géométrique du Conjugué

Dans le plan complexe, le conjugué d'un nombre complexe z est le symétrique de z par rapport à l'axe des réels. Si z est représenté par le point M d'affixe z, alors z̄ est représenté par le point M' d'affixe z̄, où M' est le symétrique de M par rapport à l'axe des abscisses.

Propriétés du Conjugué

• z̄̄ = z (le conjugué du conjugué est le nombre complexe lui-même).
• z + z̄ = 2Re(z) (la somme d'un nombre complexe et de son conjugué est le double de sa partie réelle).
• z - z̄ = 2iIm(z) (la différence d'un nombre complexe et de son conjugué est le double de sa partie imaginaire multiplié par i).
• z * z̄ = a² + b² (le produit d'un nombre complexe et de son conjugué est un nombre réel égal à la somme des carrés de sa partie réelle et de sa partie imaginaire).
• Si z = a + ib et w = c + id, alors (z + w)̄ = z̄ + w̄ et (z * w)̄ = z̄ * w̄.

Définition du Module d'un Nombre Complexe

Soit z = a + ib un nombre complexe. Le module de z, noté |z|, est défini comme la distance de l'origine du plan complexe au point d'affixe z. Mathématiquement, |z| = √(a² + b²).

Exemples de Calcul de Modules

• Si z = 3 + 4i, alors |z| = √(3² + 4²) = √(9 + 16) = √25 = 5.
• Si z = -5 - 12i, alors |z| = √((-5)² + (-12)²) = √(25 + 144) = √169 = 13.
• Si z = 7 (un nombre réel), alors |z| = √7² = 7.
• Si z = -6i (un imaginaire pur), alors |z| = √((-6)²) = 6.

Interprétation Géométrique du Module

Dans le plan complexe, le module |z| représente la longueur du vecteur reliant l'origine (0, 0) au point d'affixe z. C'est donc la distance de ce point à l'origine.

Propriétés du Module

• |z| ≥ 0 (le module est toujours un nombre réel positif ou nul).
• |z| = 0 si et seulement si z = 0.
• |z̄| = |z| (le module d'un nombre complexe est égal au module de son conjugué).
• |z * w| = |z| * |w| (le module d'un produit est le produit des modules).
• |z / w| = |z| / |w| (le module d'un quotient est le quotient des modules, à condition que w ≠ 0).
• |zⁿ| = |z|ⁿ (le module d'une puissance est la puissance du module, pour tout entier n).

Lien entre Conjugué et Module

Nous avons vu que z * z̄ = a² + b² et que |z| = √(a² + b²). Par conséquent, |z|² = z * z̄. On peut donc écrire |z| = √(z * z̄). Cette relation est très utile pour simplifier des calculs et pour déterminer l'inverse d'un nombre complexe.

Application : Calcul de l'Inverse d'un Nombre Complexe

Soit z ≠ 0 un nombre complexe. Son inverse, noté 1/z, peut être calculé en utilisant le conjugué et le module. On a 1/z = z̄ / |z|².
Exemple: Si z = 2 + 3i, alors z̄ = 2 - 3i et |z|² = 2² + 3² = 4 + 9 = 13. Donc, 1/z = (2 - 3i) / 13 = (2/13) - (3/13)i.

Ce qu'il faut retenir

• Conjugué : Si z = a + ib, alors z̄ = a - ib. C'est la symétrie par rapport à l'axe des réels dans le plan complexe.
• Module : Si z = a + ib, alors |z| = √(a² + b²). C'est la distance à l'origine dans le plan complexe.
• Lien : |z|² = z * z̄, ce qui permet de calculer l'inverse d'un nombre complexe : 1/z = z̄ / |z|².
• Le conjugué et le module sont des outils essentiels pour manipuler les nombres complexes et résoudre des équations.