Mathématiques > Géométrie > Géométrie Analytique > Utilisation des coordonnées pour résoudre des problèmes géométriques

Vérification de l'alignement de points avec les coordonnées

Apprenez à utiliser les coordonnées pour déterminer si des points sont alignés ou pour prouver des propriétés géométriques.

Concept d'alignement de points

Trois points (ou plus) sont dits alignés s'ils appartiennent à la même droite. En géométrie analytique, nous pouvons utiliser les coordonnées de ces points pour vérifier s'ils sont alignés. Cette vérification repose sur le concept de pente. Si les points A, B et C sont alignés, alors la pente de la droite (AB) doit être égale à la pente de la droite (BC). Ceci est dû au fait qu'ils se trouvent sur la même droite et ont donc la même inclinaison.

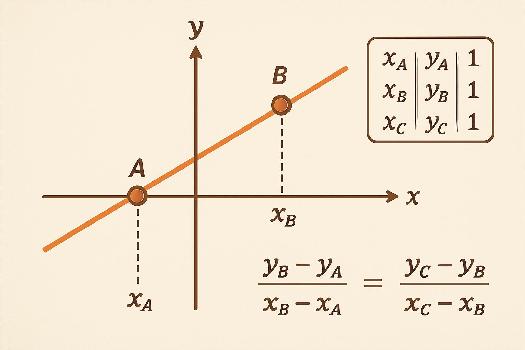
Méthode utilisant les pentes

Soient trois points A(xA, yA), B(xB, yB) et C(xC, yC). Pour vérifier si ces points sont alignés, nous calculons les pentes des droites (AB) et (BC). La pente de (AB) est donnée par mAB = (yB - yA) / (xB - xA). La pente de (BC) est donnée par mBC = (yC - yB) / (xC - xB). Si mAB = mBC, alors les points A, B et C sont alignés. Il est important de noter que xB - xA et xC - xB ne doivent pas être égaux à zéro, sinon les pentes ne sont pas définies (droites verticales). Dans ce cas, il faudrait vérifier si tous les points ont la même abscisse.

Exemple concret

Considérons les points A(1, 2), B(3, 6) et C(5, 10). Vérifions s'ils sont alignés. Calculons la pente de (AB): mAB = (6 - 2) / (3 - 1) = 4 / 2 = 2. Calculons la pente de (BC): mBC = (10 - 6) / (5 - 3) = 4 / 2 = 2. Puisque mAB = mBC = 2, les points A, B et C sont alignés.

Méthode alternative : Utilisation du déterminant

Une autre méthode pour vérifier l'alignement de trois points A(xA, yA), B(xB, yB) et C(xC, yC) consiste à utiliser le déterminant de la matrice suivante: | xA yA 1 | | xB yB 1 | | xC yC 1 | Les points A, B et C sont alignés si et seulement si ce déterminant est égal à zéro. Le déterminant se calcule comme suit: D = xA(yB - yC) + xB(yC - yA) + xC(yA - yB) Si D = 0, les points sont alignés.

Avantages et inconvénients des méthodes

  • Méthode des pentes : Simple à comprendre et à calculer, mais nécessite une attention particulière lorsque les points ont la même abscisse (droites verticales).
  • Méthode du déterminant : Plus générale et ne nécessite pas de traitement particulier pour les droites verticales. Elle est plus robuste numériquement.
Le choix de la méthode dépend du contexte et de la préférence personnelle.

Application : Démonstration de propriétés géométriques

L'alignement de points peut être utilisé pour démontrer des propriétés géométriques. Par exemple, on peut démontrer que le milieu de deux côtés d'un triangle et le milieu du troisième côté sont alignés avec le sommet opposé. Cela permet de résoudre de nombreux problèmes de géométrie de manière algébrique, ce qui est souvent plus simple et plus rigoureux que les méthodes de géométrie pure.

Ce qu'il faut retenir

  • Alignement de points : Trois points sont alignés s'ils appartiennent à la même droite.
  • Méthode des pentes : Calculer les pentes des droites (AB) et (BC). Si elles sont égales, les points sont alignés. mAB = (yB - yA) / (xB - xA) et mBC = (yC - yB) / (xC - xB).
  • Méthode du déterminant : Calculer le déterminant de la matrice formée par les coordonnées des points. S'il est égal à zéro, les points sont alignés.
  • L'alignement de points peut être utilisé pour démontrer des propriétés géométriques.

← Vecteurs dans l'espace : Définition, Opérations et Colinéarité Équations de Droites : Cartésiennes et Paramétriques →

FAQ

  • Que faire si les dénominateurs des pentes sont nuls ?

    Si le dénominateur d'une pente est nul (par exemple, xB - xA = 0), cela signifie que la droite est verticale. Dans ce cas, pour vérifier l'alignement, vérifiez simplement si tous les points ont la même abscisse.
  • Est-ce que ces méthodes fonctionnent pour plus de trois points ?

    Non, ces méthodes sont conçues pour vérifier l'alignement de trois points. Pour plus de trois points, vous devez vérifier l'alignement de chaque triplet de points.
  • Y a-t-il d'autres applications de l'alignement de points en géométrie analytique ?

    Oui, l'alignement de points est utilisé dans de nombreux problèmes, notamment pour démontrer des théorèmes géométriques, vérifier si des points appartiennent à une même figure géométrique (comme une droite ou un cercle), et résoudre des problèmes de construction géométrique.