Mathématiques > Graphes (Terminale - Spécialité) > Introduction aux Graphes > Types de graphes (orientés, non orientés, pondérés)
Introduction aux Types de Graphes
Découvrez les différents types de graphes : orientés, non orientés et pondérés. Comprenez leurs caractéristiques, leurs applications et comment les distinguer.
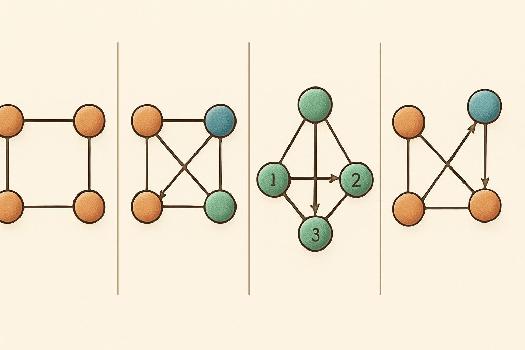
Qu'est-ce qu'un Graphe ? Rappel
Un graphe est une structure de données mathématique utilisée pour représenter des relations entre des objets. Il est constitué de sommets (ou nœuds) et d'arêtes (ou liens) qui relient ces sommets. Imaginez un réseau de villes reliées par des routes : chaque ville est un sommet, et chaque route est une arête.
Graphes Orientés
Dans un graphe orienté, les arêtes ont une direction. Cela signifie que la relation entre deux sommets n'est pas forcément réciproque. On représente une arête orientée par une flèche allant d'un sommet à un autre.
Par exemple, un graphe orienté pourrait représenter un réseau de rues à sens unique. Si une rue va de la ville A à la ville B, on peut aller de A à B, mais pas nécessairement de B à A.
Applications : Modélisation de flux (réseaux sociaux, flux de données), planification de tâches (dépendances entre tâches), etc.
Représentation : Une matrice d'adjacence d'un graphe orienté n'est pas nécessairement symétrique.
Graphes Non Orientés
Dans un graphe non orienté, les arêtes n'ont pas de direction. La relation entre deux sommets est réciproque. On représente une arête non orientée par une simple ligne entre deux sommets.
Par exemple, un graphe non orienté pourrait représenter un réseau d'amis. Si A est ami avec B, alors B est aussi ami avec A.
Applications : Représentation de réseaux sociaux (liens d'amitié), carte routière (routes bidirectionnelles), etc.
Représentation : La matrice d'adjacence d'un graphe non orienté est toujours symétrique.
Graphes Pondérés
Un graphe pondéré est un graphe où chaque arête est associée à un poids (une valeur numérique). Ce poids peut représenter une distance, un coût, une capacité, ou toute autre quantité significative.
Par exemple, un graphe pondéré pourrait représenter un réseau routier où le poids de chaque arête correspond à la distance entre deux villes.
Applications : Recherche du plus court chemin (GPS), optimisation de réseaux (télécommunications, transport), etc.
Exemple : Un algorithme comme Dijkstra est utilisé pour trouver le plus court chemin dans un graphe pondéré.
Combiner les Types
Il est possible de combiner ces types de graphes. Par exemple, on peut avoir un graphe orienté et pondéré, où les arêtes ont une direction et un poids. Cela permet de modéliser des situations encore plus complexes.
Tableau comparatif
| Type de Graphe | Direction des Arêtes | Poids des Arêtes | Représentation | Exemple d'Application |
|---|---|---|---|---|
| Orienté | Oui | Non (peut être pondéré) | Flèche | Réseau social (suivre quelqu'un) |
| Non Orienté | Non | Non (peut être pondéré) | Ligne | Réseau d'amis |
| Pondéré | Orienté ou Non Orienté | Oui | Nombre associé à l'arête | GPS (distance entre villes) |
Ce qu'il faut retenir
- Graphe : Ensemble de sommets reliés par des arêtes.
- Graphe Orienté : Arêtes avec direction (flèches). Utile pour modéliser des relations non réciproques.
- Graphe Non Orienté : Arêtes sans direction (lignes). Utile pour modéliser des relations réciproques.
- Graphe Pondéré : Arêtes avec un poids (valeur numérique). Utile pour représenter des coûts, des distances, etc.
- Il est possible de combiner ces différents types de graphes.
FAQ
-
Quelle est la différence entre un graphe orienté et un graphe non orienté ?
Dans un graphe orienté, les arêtes ont une direction (flèches), tandis que dans un graphe non orienté, les arêtes n'ont pas de direction (lignes). -
Qu'est-ce que le poids d'une arête dans un graphe pondéré ?
Le poids d'une arête représente une valeur numérique associée à cette arête, comme une distance, un coût, ou une capacité. -
Peut-on avoir un graphe orienté et pondéré ?
Oui, il est tout à fait possible d'avoir un graphe orienté et pondéré, où les arêtes ont à la fois une direction et un poids.
