Mathématiques > Géométrie > Géométrie Spatiale > Droites et plans dans l'espace (équations paramétriques et cartésiennes)

Droites et plans dans l'espace : équations paramétriques et cartésiennes

Explorez les équations paramétriques et cartésiennes des droites et des plans dans l'espace. Apprenez à les déterminer et à les utiliser pour résoudre des problèmes de géométrie spatiale.

Introduction

Bienvenue dans le monde fascinant de la géométrie spatiale ! Ici, nous allons explorer les droites et les plans, deux objets fondamentaux, et apprendre à les décrire mathématiquement à l'aide d'équations. Comprendre ces équations est essentiel pour résoudre une variété de problèmes, allant de la détermination de l'intersection de deux plans à la modélisation d'objets 3D.

Équations paramétriques d'une droite

Concept fondamental : Une droite dans l'espace est définie de manière unique par un point qu'elle contient et un vecteur directeur. Le vecteur directeur indique la direction de la droite.

Équation paramétrique : Soit un point A(xA, yA, zA) appartenant à la droite et un vecteur directeur u(a, b, c). Alors, tout point M(x, y, z) de la droite peut être décrit par les équations paramétriques suivantes :

x = xA + ta
y = yA + tb
z = zA + tc

où 't' est un paramètre réel. Chaque valeur de 't' correspond à un point différent sur la droite.

Exemple : Déterminons les équations paramétriques de la droite passant par le point A(1, 2, 3) et de vecteur directeur u(4, -1, 0).

x = 1 + 4t
y = 2 - t
z = 3

Remarquez que la coordonnée z est constante (z = 3), ce qui signifie que la droite est parallèle au plan (xOy).

Équation cartésienne d'un plan

Concept fondamental : Un plan est défini de manière unique par un point qu'il contient et un vecteur normal. Le vecteur normal est perpendiculaire au plan.

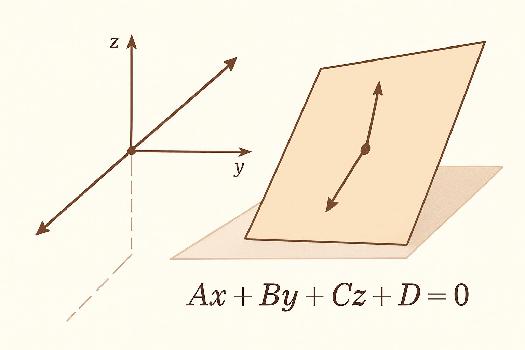
Équation cartésienne : Soit un point A(xA, yA, zA) appartenant au plan et un vecteur normal n(a, b, c). Alors, tout point M(x, y, z) du plan satisfait l'équation cartésienne suivante :

a(x - xA) + b(y - yA) + c(z - zA) = 0

On peut réécrire cette équation sous la forme plus générale :

ax + by + cz + d = 0

où d = -(axA + byA + czA).

Exemple : Déterminons l'équation cartésienne du plan passant par le point A(2, -1, 1) et de vecteur normal n(3, 2, -1).

3(x - 2) + 2(y + 1) - 1(z - 1) = 0
3x - 6 + 2y + 2 - z + 1 = 0
3x + 2y - z - 3 = 0

Donc, l'équation cartésienne du plan est 3x + 2y - z - 3 = 0.

Passage de la forme paramétrique à la forme cartésienne (et vice versa)

Il est possible de passer d'une représentation paramétrique à une représentation cartésienne, et inversement, bien que le passage de cartésien à paramétrique soit parfois plus complexe.

De paramétrique à cartésien (Droite vers Plan) : On utilise souvent cette transformation pour déterminer si une droite (donnée sous forme paramétrique) est incluse dans un plan (donné sous forme cartésienne). On substitue les équations paramétriques de la droite dans l'équation cartésienne du plan. Si l'équation est toujours vérifiée, alors la droite est incluse dans le plan.

De cartésien à paramétrique (Plan vers Droite) : On peut exprimer deux des variables (par exemple, x et y) en fonction de la troisième (z). On pose alors z = t (paramètre) et on obtient les équations paramétriques. Notez qu'il existe une infinité de représentations paramétriques possibles pour un même plan.

Applications

Les équations paramétriques et cartésiennes des droites et des plans sont utilisées dans de nombreux domaines, notamment :

  • Infographie : Modélisation d'objets 3D et rendu d'images.
  • Robotique : Planification de trajectoires de robots.
  • Physique : Description du mouvement des objets dans l'espace.
  • Géométrie : Résolution de problèmes géométriques complexes, comme la détermination de l'intersection de deux plans ou la distance d'un point à un plan.

Ce qu'il faut retenir

  • Une droite dans l'espace est définie par un point et un vecteur directeur.
  • Un plan dans l'espace est défini par un point et un vecteur normal.
  • Les équations paramétriques d'une droite expriment les coordonnées de chaque point de la droite en fonction d'un paramètre.
  • L'équation cartésienne d'un plan relie les coordonnées de chaque point du plan.
  • Il est possible de passer de la représentation paramétrique à la représentation cartésienne et inversement.
  • Ces équations sont essentielles pour résoudre des problèmes de géométrie spatiale et ont de nombreuses applications pratiques.

← Distance entre deux points dans un repère orthonormé Démonstration et applications avancées de la distance entre deux points →

FAQ

  • Comment trouver le vecteur directeur d'une droite définie par deux points ?

    Si A et B sont deux points de la droite, le vecteur AB est un vecteur directeur de la droite. Il suffit de calculer les coordonnées du vecteur AB en faisant la différence entre les coordonnées de B et celles de A.
  • Comment vérifier si un point appartient à un plan donné par son équation cartésienne ?

    Il suffit de remplacer les coordonnées du point dans l'équation cartésienne du plan. Si l'équation est vérifiée, alors le point appartient au plan.
  • Deux plans sont-ils parallèles ?

    Deux plans sont parallèles si leurs vecteurs normaux sont colinéaires, c'est-à-dire si l'un est un multiple de l'autre.