Mathématiques > Géométrie > Géométrie Plane > Angles et trigonométrie dans le triangle rectangle

Angles et Trigonométrie dans le Triangle Rectangle : Guide Complet

Explorez en détail les relations trigonométriques fondamentales dans le triangle rectangle : sinus, cosinus, tangente. Ce guide complet vous fournira les outils nécessaires pour maîtriser ces concepts essentiels, avec des exemples concrets et des exercices d'application pour consolider votre apprentissage.

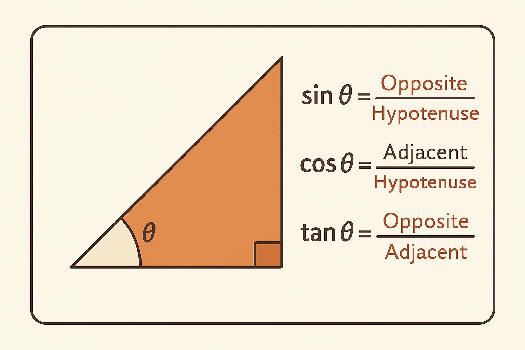
Introduction au Triangle Rectangle

Le triangle rectangle est une figure géométrique fondamentale. Un triangle rectangle est un triangle qui possède un angle droit, c'est-à-dire un angle mesurant exactement 90 degrés. Le côté opposé à l'angle droit est appelé l'hypoténuse, et c'est toujours le côté le plus long du triangle. Les deux autres côtés sont appelés les côtés adjacents à l'angle droit ou simplement les côtés.

Définition des Rapports Trigonométriques

Les rapports trigonométriques relient les angles d'un triangle rectangle aux longueurs de ses côtés. Les trois principaux rapports trigonométriques sont:

  • Sinus (sin) : Le sinus d'un angle aigu est le rapport de la longueur du côté opposé à cet angle à la longueur de l'hypoténuse. sin(θ) = Côté Opposé / Hypoténuse
  • Cosinus (cos) : Le cosinus d'un angle aigu est le rapport de la longueur du côté adjacent à cet angle à la longueur de l'hypoténuse. cos(θ) = Côté Adjacent / Hypoténuse
  • Tangente (tan) : La tangente d'un angle aigu est le rapport de la longueur du côté opposé à cet angle à la longueur du côté adjacent. tan(θ) = Côté Opposé / Côté Adjacent
Il est important de se souvenir de ces définitions. Un moyen mnémotechnique courant est SOH CAH TOA, où:

  • SOH : Sinus = Opposé / Hypoténuse
  • CAH : Cosinus = Adjacent / Hypoténuse
  • TOA : Tangente = Opposé / Adjacent

Angles Complémentaires et Trigonométrie

Dans un triangle rectangle, les deux angles aigus sont complémentaires, ce qui signifie que leur somme est égale à 90 degrés. Si on a un triangle ABC rectangle en B, alors l'angle en A et l'angle en C sont complémentaires.

Il existe des relations importantes entre les sinus, cosinus et tangentes des angles complémentaires. Si α et β sont deux angles complémentaires (α + β = 90°), alors:

  • sin(α) = cos(β)
  • cos(α) = sin(β)
  • tan(α) = 1 / tan(β) ou tan(α) * tan(β) = 1
Ces relations sont utiles pour simplifier des expressions trigonométriques et résoudre des problèmes.

Applications et Exemples Concrets

La trigonométrie du triangle rectangle a de nombreuses applications dans des domaines tels que la navigation, l'ingénierie, la physique et l'architecture. Voici quelques exemples:

  1. Calcul de la hauteur d'un bâtiment: En mesurant l'angle d'élévation du sommet d'un bâtiment à partir d'un point donné et en connaissant la distance de ce point à la base du bâtiment, on peut utiliser la tangente pour calculer la hauteur du bâtiment.
  2. Navigation: Les marins utilisent la trigonométrie pour déterminer leur position et leur direction en mer.
  3. Ingénierie: Les ingénieurs utilisent la trigonométrie pour concevoir des ponts, des bâtiments et d'autres structures.
Exemple 1:
Un triangle rectangle ABC est rectangle en B. On donne AB = 5 cm et l'angle en A = 30°. Calculer la longueur de BC.

Solution:
On a tan(A) = BC / AB, donc BC = AB * tan(A) = 5 * tan(30°) ≈ 2.89 cm.

Exemple 2:
Dans un triangle rectangle DEF, on donne DE = 8 cm et EF = 6 cm. Calculer la mesure de l'angle en D.

Solution:
On a tan(D) = EF / DE = 6 / 8 = 0.75. Donc, D = arctan(0.75) ≈ 36.87°.

Résolution de problèmes avec la trigonométrie

Pour résoudre des problèmes impliquant la trigonométrie dans un triangle rectangle, suivez ces étapes:

  1. Identifier l'angle de référence.
  2. Identifier les côtés connus (opposé, adjacent, hypoténuse).
  3. Choisir le rapport trigonométrique approprié (sin, cos, tan) qui relie les côtés connus à l'inconnu.
  4. Écrire l'équation et la résoudre pour trouver l'inconnue.
  5. Vérifier que la réponse est raisonnable dans le contexte du problème.

Ce qu'il faut retenir

  • Définition du triangle rectangle: Un triangle avec un angle de 90 degrés. Le côté opposé à l'angle droit est l'hypoténuse, le plus long côté.
  • Rapports trigonométriques:
    • sin(θ) = Côté Opposé / Hypoténuse
    • cos(θ) = Côté Adjacent / Hypoténuse
    • tan(θ) = Côté Opposé / Côté Adjacent
  • Moyen mnémotechnique: SOH CAH TOA.
  • Angles complémentaires: Si α + β = 90°, alors sin(α) = cos(β) et cos(α) = sin(β).
  • Applications: Calcul de hauteurs, navigation, ingénierie.

← Angles Orientés et Mesure en Radians : Un Guide Complet Applications des Vecteurs en Géométrie Plane →

FAQ

  • Comment choisir le bon rapport trigonométrique (sin, cos, tan) pour résoudre un problème ?

    Identifiez l'angle de référence, les côtés connus (opposé, adjacent, hypoténuse) et choisissez le rapport qui relie les côtés connus à l'inconnue.
  • Quelle est la relation entre le sinus et le cosinus d'angles complémentaires ?

    Si deux angles α et β sont complémentaires (α + β = 90°), alors sin(α) = cos(β) et cos(α) = sin(β).