Inéquations du premier degré : Guide de résolution

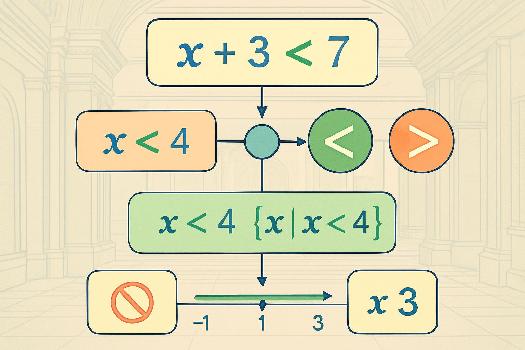
Introduction aux inéquations

Une inéquation est une expression mathématique qui relie deux quantités en utilisant des symboles d'inégalité : <, >, ≤, ou ≥. Contrairement aux équations qui recherchent une valeur unique, les inéquations déterminent un intervalle de valeurs qui satisfont la condition donnée. Par exemple, x > 3 signifie que x peut prendre n'importe quelle valeur supérieure à 3.

Vocabulaire et notations

• Membre de gauche : L'expression située à gauche du symbole d'inégalité.
• Membre de droite : L'expression située à droite du symbole d'inégalité.
• Sens de l'inégalité : Indique la relation entre les deux membres (<, >, ≤, ≥).
• Solution d'une inéquation : Toute valeur de l'inconnue qui vérifie l'inégalité.

Règles de manipulation des inéquations

Les inéquations peuvent être manipulées en respectant certaines règles, similaires à celles des équations, mais avec une attention particulière au sens de l'inégalité.

1. Addition/Soustraction : On peut ajouter ou soustraire la même quantité aux deux membres d'une inéquation sans changer le sens de l'inégalité. Si a < b, alors a + c < b + c et a - c < b - c.
2. Multiplication/Division par un nombre positif : On peut multiplier ou diviser les deux membres d'une inéquation par un nombre positif sans changer le sens de l'inégalité. Si a < b et c > 0, alors ac < bc et a/c < b/c.
3. Multiplication/Division par un nombre négatif : On peut multiplier ou diviser les deux membres d'une inéquation par un nombre négatif, MAIS on doit inverser le sens de l'inégalité. Si a < b et c < 0, alors ac > bc et a/c > b/c.

Résolution d'une inéquation du premier degré

La résolution d'une inéquation du premier degré consiste à isoler l'inconnue (généralement 'x') d'un côté de l'inégalité. Suivez ces étapes:

1. Simplifier l'inéquation : Développer et réduire chaque membre de l'inéquation.
2. Isoler le terme en 'x' : Ajouter ou soustraire des termes constants pour regrouper les termes en 'x' d'un côté et les constantes de l'autre.
3. Diviser pour isoler 'x' : Diviser les deux membres par le coefficient de 'x'. N'oubliez pas d'inverser le sens de l'inégalité si vous divisez par un nombre négatif.
4. Exprimer la solution : Exprimer la solution sous forme d'intervalle ou sur une droite numérique.

Exemple détaillé

Résolvons l'inéquation suivante: 3x + 5 < 7x - 3

1. Étape 1: Soustrayez 3x des deux côtés: 5 < 4x - 3
2. Étape 2: Ajoutez 3 aux deux côtés: 8 < 4x
3. Étape 3: Divisez les deux côtés par 4: 2 < x (ou x > 2)

Représentation graphique

La solution d'une inéquation peut être représentée graphiquement sur une droite numérique. Pour l'exemple précédent (x > 2), on trace une droite numérique, on place un cercle ouvert (car 2 n'est pas inclus) sur le point 2, et on hachure la partie de la droite à droite du cercle, indiquant que toutes ces valeurs sont des solutions.

Pour une inéquation du type x ≥ 2, le cercle serait fermé (ou un crochet) pour indiquer que 2 est inclus dans la solution.

Cas particuliers

• Inéquations sans solution: Parfois, une inéquation peut mener à une contradiction. Par exemple, 0 < -5. Dans ce cas, l'inéquation n'a aucune solution.
• Inéquations toujours vraies: De même, une inéquation peut toujours être vraie, quel que soit la valeur de x. Par exemple, 0 > -5. Dans ce cas, tous les nombres réels sont des solutions.

Ce qu'il faut retenir

• Une inéquation relie deux expressions avec des symboles d'inégalité (<, >, ≤, ≥).
• Pour résoudre une inéquation, on isole l'inconnue en utilisant des opérations mathématiques.
• Si on multiplie ou divise par un nombre négatif, on inverse le sens de l'inégalité.
• La solution peut être exprimée sous forme d'intervalle ou représentée graphiquement sur une droite numérique.
• Les cas particuliers incluent les inéquations sans solution et les inéquations toujours vraies.