Résolution d'équations diophantiennes linéaires

Introduction aux équations diophantiennes linéaires

Les équations diophantiennes sont des équations polynomiales où l'on recherche des solutions entières (relatives). Une équation diophantienne linéaire prend la forme ax + by = c, où a, b et c sont des entiers donnés et x et y sont les inconnues que nous cherchons à déterminer, également entières.

Théorème de Bézout

Le théorème de Bézout est un outil fondamental pour la résolution d'équations diophantiennes linéaires. Il stipule que pour deux entiers a et b, il existe des entiers x et y tels que ax + by = pgcd(a, b), où pgcd(a, b) désigne le plus grand diviseur commun de a et b.

Exemple: Soit a = 12 et b = 18. Alors pgcd(12, 18) = 6. On peut trouver des entiers x et y tels que 12x + 18y = 6. Par exemple, x = -1 et y = 1 fonctionnent : 12(-1) + 18(1) = -12 + 18 = 6.

Condition d'existence des solutions

L'équation diophantienne linéaire ax + by = c admet des solutions entières si et seulement si pgcd(a, b) divise c. Autrement dit, c doit être un multiple de pgcd(a, b). Si cette condition n'est pas remplie, l'équation n'a pas de solutions entières.

Exemple 1: L'équation 6x + 9y = 15 admet des solutions car pgcd(6, 9) = 3 et 3 divise 15.

Exemple 2: L'équation 6x + 9y = 16 n'admet pas de solutions car pgcd(6, 9) = 3 et 3 ne divise pas 16.

Méthode de résolution

Voici les étapes pour résoudre une équation diophantienne linéaire ax + by = c :

1. Calculer le pgcd(a, b) : Utiliser l'algorithme d'Euclide pour trouver le plus grand diviseur commun de a et b.
2. Vérifier la condition d'existence : Vérifier si pgcd(a, b) divise c. Si ce n'est pas le cas, l'équation n'a pas de solutions.
3. Trouver une solution particulière (x₀, y₀) : Utiliser le théorème de Bézout pour trouver des entiers x' et y' tels que ax' + by' = pgcd(a, b). Ensuite, si c = k * pgcd(a, b), alors x₀ = k * x' et y₀ = k * y' est une solution particulière de l'équation ax + by = c. L'algorithme d'Euclide étendu permet de trouver facilement x' et y'.
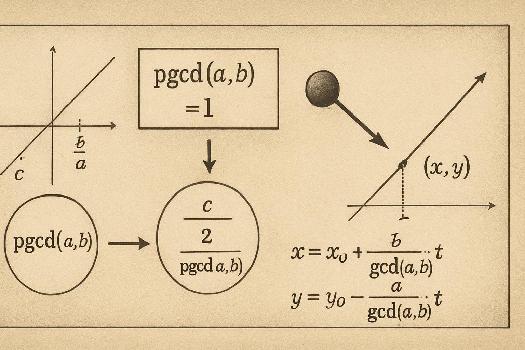
4. Exprimer les solutions générales : Si (x₀, y₀) est une solution particulière, alors toutes les solutions sont de la forme :
   x = x₀ + (b/pgcd(a, b)) * t
   y = y₀ - (a/pgcd(a, b)) * t
   où t est un entier relatif quelconque.

Exemple détaillé

Résolvons l'équation 7x + 5y = 1.

1. Calcul du pgcd(7, 5) : En utilisant l'algorithme d'Euclide :
   7 = 1 * 5 + 2
   5 = 2 * 2 + 1
   2 = 2 * 1 + 0
   Donc pgcd(7, 5) = 1.
2. Vérification de la condition d'existence : Puisque pgcd(7, 5) = 1 et 1 divise 1, l'équation admet des solutions.
3. Trouver une solution particulière : Remontons l'algorithme d'Euclide :
   1 = 5 - 2 * 2
   1 = 5 - 2 * (7 - 1 * 5)
   1 = 5 - 2 * 7 + 2 * 5
   1 = 3 * 5 - 2 * 7
   Donc 7 * (-2) + 5 * (3) = 1. Une solution particulière est (x₀, y₀) = (-2, 3).
4. Exprimer les solutions générales : Les solutions générales sont de la forme :
   x = -2 + (5/1) * t = -2 + 5t
   y = 3 - (7/1) * t = 3 - 7t
   où t est un entier relatif quelconque.

Ce qu'il faut retenir

• Une équation diophantienne linéaire est de la forme ax + by = c.
• Le théorème de Bézout est crucial pour trouver des solutions.
• L'équation a des solutions si et seulement si pgcd(a, b) divise c.
• La méthode de résolution comprend le calcul du pgcd, la vérification de l'existence de solutions, la recherche d'une solution particulière et l'expression des solutions générales.