Intégrale Définie : Comprendre l'Aire Sous une Courbe

Introduction à l'Intégrale Définie

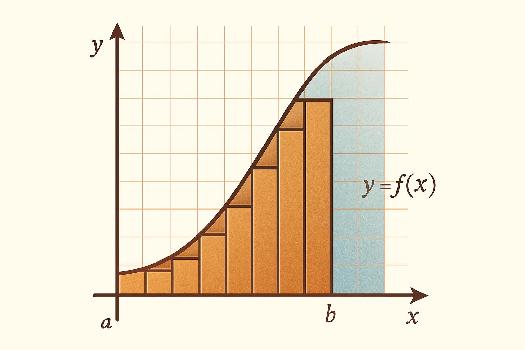
L'intégrale définie est un concept fondamental en analyse. Elle nous permet de calculer l'aire algébrique sous une courbe entre deux bornes, disons a et b. En termes simples, imaginez une fonction f(x) tracée sur un graphique. L'intégrale définie de f(x) de a à b représente l'aire délimitée par la courbe de f(x), l'axe des x, et les droites verticales x = a et x = b. Il est important de noter que l'aire au-dessus de l'axe des x est considérée positive, tandis que l'aire en dessous est considérée négative.

Calcul Approximatif de l'Aire : la Méthode des Rectangles

Avant de plonger dans le calcul formel, visualisons comment on peut *approximer* cette aire. Une méthode intuitive est de diviser l'intervalle [a, b] en plusieurs petits rectangles. Plus il y a de rectangles, meilleure est l'approximation. Pour chaque rectangle, sa base est la largeur de l'intervalle (b-a) divisée par le nombre de rectangles, et sa hauteur est la valeur de la fonction en un point quelconque de cet intervalle (par exemple, le point milieu). La somme des aires de tous ces rectangles donne une approximation de l'intégrale définie.

Exemple : Pour approcher l'aire sous la courbe de f(x) = x² entre 0 et 1 avec 4 rectangles, on diviserait l'intervalle [0, 1] en quatre sous-intervalles : [0, 0.25], [0.25, 0.5], [0.5, 0.75], et [0.75, 1]. On pourrait utiliser le point milieu de chaque intervalle pour déterminer la hauteur du rectangle. Ensuite, on calcule l'aire de chaque rectangle (base x hauteur) et on les additionne.

La Définition Formelle de l'Intégrale Définie

Mathématiquement, l'intégrale définie est définie comme la limite de la somme de Riemann lorsque le nombre de rectangles tend vers l'infini et que la largeur de chaque rectangle tend vers zéro. C'est une définition rigoureuse qui nous permet de calculer l'aire sous une courbe avec une précision infinie.

Soit f une fonction continue sur [a, b]. L'intégrale définie de f de a à b, notée ∫_a^b f(x) dx, est définie par:

∫_a^b f(x) dx = lim_n→∞ Σ_i=1ⁿ f(x_i) Δx

où Δx = (b-a)/n et x_i est un point dans le i-ème sous-intervalle. La notation ∫ est le symbole d'intégration, f(x) est la fonction à intégrer (appelée intégrande), a est la borne inférieure d'intégration, b est la borne supérieure d'intégration, et dx indique la variable d'intégration.

Le Théorème Fondamental du Calcul

Le théorème fondamental du calcul établit un lien crucial entre la dérivation et l'intégration. Il affirme que si F(x) est une primitive de f(x) (c'est-à-dire, F'(x) = f(x)), alors l'intégrale définie de f(x) de a à b est égale à la différence entre la valeur de F(x) en b et sa valeur en a:

∫_a^b f(x) dx = F(b) - F(a)

Cela signifie que pour calculer l'intégrale définie, il suffit de trouver une primitive de la fonction, d'évaluer cette primitive aux bornes d'intégration, et de soustraire les résultats. C'est une méthode bien plus simple que de passer par la définition de la somme de Riemann!

Exemple : Calculons ∫₀¹ x² dx. Une primitive de x² est (1/3)x³. Donc, ∫₀¹ x² dx = (1/3)(1)³ - (1/3)(0)³ = 1/3.

Propriétés de l'Intégrale Définie

L'intégrale définie possède plusieurs propriétés utiles :

• Linéarité: ∫_a^b [cf(x) + dg(x)] dx = c∫_a^b f(x) dx + d∫_a^b g(x) dx, où c et d sont des constantes.
• Additivité par rapport à l'intervalle d'intégration: ∫_a^b f(x) dx + ∫_b^c f(x) dx = ∫_a^c f(x) dx
• Inversion des bornes: ∫_a^b f(x) dx = -∫_b^a f(x) dx
• Si f(x) ≥ 0 sur [a, b], alors ∫_a^b f(x) dx ≥ 0
• Si f(x) ≤ 0 sur [a, b], alors ∫_a^b f(x) dx ≤ 0

Applications de l'Intégrale Définie pour le Calcul d'Aires

L'application principale de l'intégrale définie est le calcul d'aires. Voici quelques exemples :

• Aire entre une courbe et l'axe des x: Si f(x) ≥ 0 sur [a, b], alors l'aire sous la courbe de f(x) entre a et b est donnée par ∫_a^b f(x) dx. Si f(x) ≤ 0 sur [a, b], alors l'aire est donnée par -∫_a^b f(x) dx. Pour une fonction qui change de signe, il faut diviser l'intervalle en sections où f(x) est soit positive soit négative, et sommer les valeurs absolues des intégrales sur ces sections.
• Aire entre deux courbes: L'aire entre deux courbes f(x) et g(x) entre a et b, où f(x) ≥ g(x) sur [a, b], est donnée par ∫_a^b [f(x) - g(x)] dx.

Ce qu'il faut retenir

• L'intégrale définie représente l'aire algébrique sous une courbe entre deux bornes.
• Elle peut être approchée par la méthode des rectangles (sommes de Riemann).
• Le théorème fondamental du calcul relie l'intégration et la dérivation, permettant un calcul plus aisé des intégrales définies.
• L'intégrale définie possède des propriétés importantes comme la linéarité et l'additivité.
• Elle est utilisée pour calculer des aires entre une courbe et l'axe des x, ou entre deux courbes.