Physique-Chimie > Optique > Optique Géométrique > Réflexion totale interne

Réflexion Totale Interne : Comprendre et Appliquer

Explication détaillée de la réflexion totale interne, un phénomène optique essentiel. Ce cours aborde les conditions d'apparition, les applications courantes et propose des exemples pour une compréhension approfondie.

Introduction à la Réflexion Totale Interne

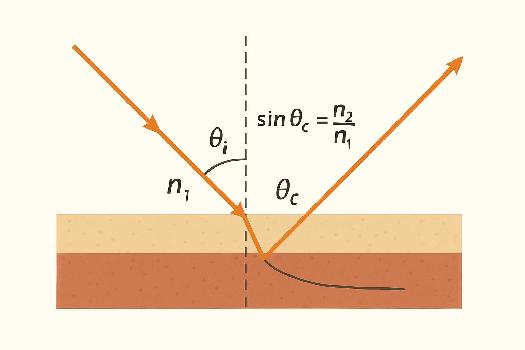
La réflexion totale interne (RTI) est un phénomène optique qui se produit lorsque la lumière se propageant dans un milieu transparent (comme l'eau ou le verre) atteint une interface avec un milieu moins réfringent (comme l'air) avec un angle d'incidence suffisamment grand. Au lieu de traverser l'interface et de se réfracter, la lumière est entièrement réfléchie à l'intérieur du milieu d'origine. C'est comme si la surface agissait comme un miroir parfait. C'est un principe fondamental derrière de nombreuses technologies, notamment les fibres optiques.

L'Indice de Réfraction et l'Angle Limite

Pour comprendre la RTI, il faut d'abord connaître l'indice de réfraction (n). L'indice de réfraction d'un milieu est une mesure de la vitesse de la lumière dans ce milieu par rapport à sa vitesse dans le vide. Plus l'indice de réfraction est élevé, plus la lumière se propage lentement dans ce milieu. L'angle d'incidence est l'angle entre le rayon lumineux incident et la normale (la ligne perpendiculaire) à la surface. L'angle limite (θc) est l'angle d'incidence au-delà duquel la réflexion totale interne se produit. Il est donné par la formule: sin(θc) = n2 / n1, où n1 est l'indice de réfraction du milieu où la lumière se propage initialement (le milieu le plus réfringent) et n2 est l'indice de réfraction du milieu vers lequel la lumière tente de passer (le milieu le moins réfringent). Si l'angle d'incidence est supérieur à l'angle limite, alors toute la lumière est réfléchie.

Conditions Nécessaires pour la Réflexion Totale Interne

Pour que la réflexion totale interne se produise, deux conditions doivent être remplies :

  1. La lumière doit se propager d'un milieu avec un indice de réfraction élevé (n1) vers un milieu avec un indice de réfraction plus faible (n2), donc n1 > n2. Par exemple, de l'eau vers l'air.
  2. L'angle d'incidence (θi) doit être supérieur à l'angle limite (θc). θi > θc.
Si ces deux conditions sont remplies, toute la lumière est réfléchie à l'intérieur du premier milieu et aucune lumière n'est réfractée à travers la surface.

Exemples et Applications de la Réflexion Totale Interne

La réflexion totale interne a de nombreuses applications pratiques, notamment:

  • Fibres Optiques : La RTI est le principe de base des fibres optiques. La lumière est guidée à travers une fibre optique en subissant de multiples réflexions totales internes. Ceci permet de transmettre des données sur de longues distances avec très peu de pertes.
  • Prismes à Réflexion Totale : Certains prismes utilisent la RTI pour dévier la lumière sans perte d'intensité. Ils sont utilisés dans les jumelles, les appareils photo et d'autres instruments optiques.
  • Mirages : Les mirages sont des illusions d'optique causées par la réfraction et la réflexion totale interne de la lumière dans des couches d'air de différentes températures.
  • Endoscopie : Les endoscopes utilisent des fibres optiques pour visualiser l'intérieur du corps humain.
Exemple concret : Imaginez un plongeur sous l'eau. En regardant vers la surface avec un angle suffisamment oblique, il verra un reflet parfait du fond de la piscine à la surface. C'est la réflexion totale interne en action.

Calcul de l'Angle Limite : Exemple

Prenons l'exemple d'un rayon lumineux qui se propage de l'eau (n1 = 1.33) vers l'air (n2 = 1.00). Pour calculer l'angle limite, on utilise la formule : sin(θc) = n2 / n1 sin(θc) = 1.00 / 1.33 sin(θc) ≈ 0.752 θc = arcsin(0.752) θc ≈ 48.8° Donc, si l'angle d'incidence du rayon lumineux dans l'eau est supérieur à 48.8°, il y aura réflexion totale interne.

Ce qu'il faut retenir

  • La réflexion totale interne se produit lorsque la lumière passe d'un milieu d'indice élevé (n1) vers un milieu d'indice faible (n2) avec un angle d'incidence supérieur à l'angle limite.
  • L'angle limite (θc) est calculé par la formule : sin(θc) = n2 / n1.
  • Les conditions pour la RTI sont : n1 > n2 et θi > θc.
  • Les applications incluent les fibres optiques, les prismes à réflexion totale, les mirages et l'endoscopie.

← Propagation Rectiligne de la Lumière : Cours Complet →

FAQ

  • Qu'est-ce qui se passe si l'angle d'incidence est exactement égal à l'angle limite ?

    Si l'angle d'incidence est égal à l'angle limite, une partie de la lumière est réfléchie et une autre partie est réfractée à 90 degrés par rapport à la normale à la surface. Le rayon réfracté se propage alors le long de la surface.
  • La réflexion totale interne se produit-elle avec toutes les longueurs d'onde de la lumière ?

    Oui, la réflexion totale interne peut se produire avec toutes les longueurs d'onde de la lumière, tant que les conditions d'indice de réfraction et d'angle d'incidence sont satisfaites. Cependant, l'indice de réfraction peut varier légèrement avec la longueur d'onde (phénomène de dispersion), ce qui peut légèrement modifier l'angle limite pour différentes couleurs de lumière.