Moment d'une force par rapport à un axe

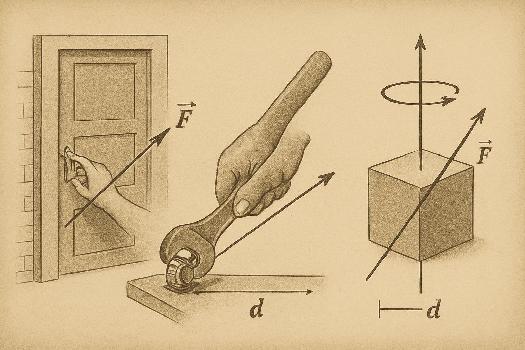
Définition du moment d'une force par rapport à un axe

Le moment d'une force par rapport à un axe est une grandeur physique qui caractérise l'aptitude de cette force à faire tourner un corps autour de cet axe. Il est essentiel de bien distinguer le moment d'une force par rapport à un point, du moment d'une force par rapport à un axe. Dans le cas du moment par rapport à un axe, on s'intéresse à la composante de la force qui a tendance à faire tourner l'objet autour de cet axe. Imaginez que vous essayez de dévisser un boulon : plus vous appliquez une force loin de l'axe du boulon, plus il est facile de le dévisser. C'est une manifestation du moment d'une force. L'unité du moment d'une force est le Newton-mètre (N·m).

Calcul du moment d'une force par rapport à un axe

Le calcul précis du moment d'une force par rapport à un axe nécessite une approche vectorielle. Cependant, dans de nombreux cas simplifiés rencontrés au lycée, nous pouvons utiliser des formules plus directes. Voici les étapes générales :

1. Identifier l'axe de rotation : Il s'agit de l'axe autour duquel le corps est susceptible de tourner.
2. Identifier la force : Déterminez la force qui agit sur le corps et dont vous voulez calculer le moment.
3. Déterminer la composante de la force perpendiculaire au plan contenant l'axe et le point d'application de la force: C'est cette composante qui contribue au moment par rapport à l'axe. Notez que cette composante peut être nulle (si la force est parallèle à l'axe ou si elle passe par l'axe)
4. Calculer le bras de levier : Le bras de levier (d) est la distance la plus courte (perpendiculaire) entre l'axe de rotation et la ligne d'action de la force (la ligne le long de laquelle la force agit).
5. Calculer le moment : Le moment (M) est alors donné par :
   M = ± F × d
   
   Où F est la norme de la composante de la force perpendiculaire, et d est le bras de levier. Le signe (+ ou -) dépend du sens de rotation que la force tend à provoquer. Par convention, on peut choisir un sens de rotation positif (par exemple, le sens trigonométrique) et attribuer le signe approprié au moment.

Exemple concret : Une porte

Prenons l'exemple d'une porte. L'axe de rotation est l'axe vertical des charnières. Si vous poussez la porte près des charnières, il faut appliquer une force importante pour la faire bouger. Si vous poussez la porte loin des charnières (près de la poignée), une force beaucoup plus faible suffit. Pourquoi ? Parce que le bras de levier est plus grand. Le moment de la force est plus important, ce qui permet une rotation plus facile. La composante de la force qui fait tourner la porte est celle qui est perpendiculaire à la porte elle-même. Si vous poussez directement dans l'axe des charnières, vous n'exercerez aucun moment (bras de levier nul).

Exemple concret : Clef à molette

Imaginez que vous essayez de desserrer un écrou rouillé avec une clé à molette. L'axe de rotation est l'axe de l'écrou. Plus la clé à molette est longue, plus il est facile de desserrer l'écrou, même en appliquant la même force. C'est parce que l'augmentation de la longueur de la clé augmente le bras de levier, et donc le moment de la force que vous appliquez. La composante de la force qui est parallèle à l'axe de l'écrou n'aura aucun effet sur sa rotation.

Signe du moment

Le moment d'une force est une grandeur algébrique, ce qui signifie qu'elle peut être positive ou négative. Le signe du moment indique le sens de rotation que la force tend à provoquer autour de l'axe. Par convention, on choisit un sens de rotation comme étant positif (par exemple, le sens trigonométrique) et on attribue le signe approprié au moment. Si la force tend à faire tourner le corps dans le sens positif, le moment est positif. Si la force tend à faire tourner le corps dans le sens négatif, le moment est négatif.

Ce qu'il faut retenir

• Le moment d'une force par rapport à un axe mesure l'efficacité d'une force à provoquer la rotation d'un corps autour de cet axe.
• Le moment dépend de la force, de la distance entre la ligne d'action de la force et l'axe (bras de levier), et de l'angle entre la force et le bras de levier.
• La formule générale est M = ± F × d, où F est la composante de la force perpendiculaire et d est le bras de levier.
• Le signe du moment indique le sens de rotation.
• L'unité du moment est le Newton-mètre (N·m).
• Des exemples concrets incluent l'ouverture d'une porte et l'utilisation d'une clé à molette.