Introduction au Mouvement Harmonique Simple (MHS)

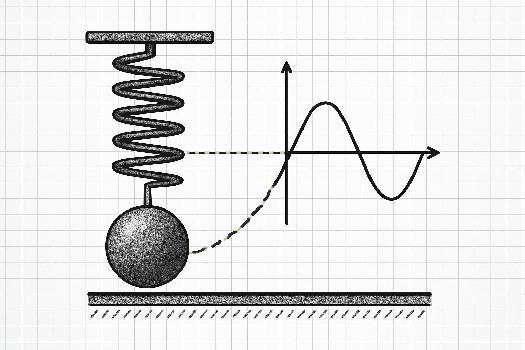
Qu'est-ce que le Mouvement Harmonique Simple ?

Le Mouvement Harmonique Simple (MHS) est un type de mouvement oscillatoire où la force de rappel est directement proportionnelle au déplacement et agit dans la direction opposée. Imaginez un ressort que vous étirez ou compressez : plus vous le déplacez de sa position d'équilibre, plus la force qui le ramène à cette position est grande.

Caractéristiques essentielles du MHS :

• Force de rappel proportionnelle au déplacement : F = -kx, où F est la force, k est la constante de raideur (du ressort, par exemple), et x est le déplacement par rapport à la position d'équilibre. Le signe moins indique que la force s'oppose au déplacement.
• Mouvement périodique : Le mouvement se répète à intervalles réguliers.
• Absence de frottement : Pour un MHS idéal, on néglige les forces de frottement. Dans la réalité, le frottement amortit le mouvement, le transformant en un mouvement harmonique amorti.

Conditions pour un MHS

Pour qu'un mouvement soit considéré comme un MHS, certaines conditions doivent être remplies :

• Présence d'une position d'équilibre stable : C'est le point où le système revient naturellement s'il est perturbé.
• Force de rappel proportionnelle au déplacement : Comme mentionné précédemment, c'est la condition la plus importante.
• Masse en mouvement : Un objet doit osciller autour de la position d'équilibre.

Exemple typique : Un bloc attaché à un ressort horizontal glissant sur une surface sans frottement. Si vous étirez le ressort et relâchez le bloc, il oscillera d'avant en arrière autour de sa position d'équilibre dans un MHS.

Équations du Mouvement Harmonique Simple

Le MHS peut être décrit mathématiquement à l'aide de fonctions trigonométriques (sinus et cosinus). Voici les équations clés :

• Déplacement (x) en fonction du temps (t) : x(t) = A cos(ωt + φ)
• A : Amplitude (déplacement maximal par rapport à la position d'équilibre).
• ω : Fréquence angulaire (en radians par seconde). ω = 2πf, où f est la fréquence en Hertz.
• t : Temps.
• φ : Phase initiale (détermine la position de départ au temps t=0).
• Vitesse (v) en fonction du temps (t) : v(t) = -Aω sin(ωt + φ)
• Accélération (a) en fonction du temps (t) : a(t) = -Aω² cos(ωt + φ) = -ω²x(t)

Période (T) et Fréquence (f) :

• Période (T) : Temps nécessaire pour effectuer une oscillation complète. T = 2π/ω.
• Fréquence (f) : Nombre d'oscillations par seconde. f = 1/T = ω/2π.

Relation avec la constante de raideur (k) et la masse (m) : ω = √(k/m), T = 2π√(m/k)

Exemples de Mouvement Harmonique Simple

Voici quelques exemples courants de systèmes qui présentent (ou approchent) un MHS :

• Masse attachée à un ressort : Déjà mentionné, c'est l'exemple le plus classique.
• Pendule simple (petites oscillations) : Pour de petits angles d'oscillation, le mouvement d'un pendule simple est une bonne approximation du MHS.
• Circuit LC (idéal) : Un circuit contenant un condensateur (C) et une bobine (L) peut osciller à une fréquence spécifique, se comportant comme un oscillateur harmonique.

Ce qu'il faut retenir

• Le Mouvement Harmonique Simple est un mouvement oscillatoire caractérisé par une force de rappel proportionnelle au déplacement.
• Les conditions pour un MHS sont : position d'équilibre stable, force de rappel proportionnelle au déplacement et masse en mouvement.
• Les équations clés du MHS sont : x(t) = A cos(ωt + φ), v(t) = -Aω sin(ωt + φ), a(t) = -ω²x(t).
• La période (T) est le temps pour une oscillation complète, et la fréquence (f) est le nombre d'oscillations par seconde.
• ω = √(k/m) où k est la constante de raideur et m la masse. T = 2π√(m/k)
• Exemples de MHS : masse-ressort, pendule simple (petites oscillations), circuit LC (idéal).