Physique-Chimie > Optique > Optique Géométrique > Lois de la réfraction (Snell-Descartes)
Les Lois de la Réfraction : Snell-Descartes
Comprendre en détail les lois de Snell-Descartes pour la réfraction de la lumière. Explications claires, exemples et exercices pour les lycéens en Physique-Chimie.
Introduction à la Réfraction
La réfraction est le phénomène par lequel une onde, comme la lumière, change de direction lorsqu'elle passe d'un milieu à un autre. Ce changement de direction est dû à la modification de la vitesse de l'onde dans le nouveau milieu. Pensez à un rayon de lumière passant de l'air à l'eau : il ne continue pas en ligne droite, mais est dévié. C'est la réfraction en action! Cette déviation est quantifiée par les lois de Snell-Descartes.
Les Indices de Réfraction
Chaque milieu transparent possède un indice de réfraction, noté 'n', qui indique à quel point la lumière est ralentie dans ce milieu par rapport au vide. L'indice de réfraction du vide est exactement 1. L'indice de réfraction de l'air est très proche de 1 (environ 1.0003), et celui de l'eau est d'environ 1.33. Plus l'indice est élevé, plus la lumière se propage lentement dans le milieu.
Voici quelques exemples d'indices de réfraction :
- Vide : n = 1
- Air : n ≈ 1.0003
- Eau : n ≈ 1.33
- Verre : n ≈ 1.5 à 1.9 (selon le type de verre)
- Diamant : n ≈ 2.42
Il est important de noter que l'indice de réfraction dépend de la longueur d'onde de la lumière. C'est ce qui provoque la dispersion de la lumière blanche à travers un prisme.
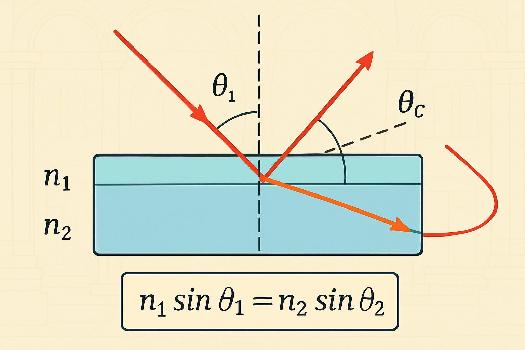
Première Loi de Snell-Descartes (Incidence et Réfraction)
La première loi de Snell-Descartes stipule que le rayon incident, la normale à la surface au point d'incidence, et le rayon réfracté sont tous situés dans le même plan. En termes simples, imaginez une feuille de papier : les trois rayons (incident, normal, réfracté) se trouvent tous sur cette même feuille. Cela permet de simplifier l'analyse de la réfraction en considérant uniquement un plan.
Deuxième Loi de Snell-Descartes (Relation des Angles)
La deuxième loi de Snell-Descartes établit une relation mathématique entre les angles d'incidence (θ1) et de réfraction (θ2) et les indices de réfraction des deux milieux (n1 et n2). Elle s'exprime par la formule suivante:
n1 sin(θ1) = n2 sin(θ2)
- n1 est l'indice de réfraction du milieu d'incidence.
- θ1 est l'angle d'incidence (l'angle entre le rayon incident et la normale).
- n2 est l'indice de réfraction du milieu de réfraction.
- θ2 est l'angle de réfraction (l'angle entre le rayon réfracté et la normale).
Cette formule permet de calculer l'angle de réfraction si l'on connaît l'angle d'incidence et les indices de réfraction des deux milieux, ou vice-versa.
Angle d'incidence et angle de réfraction
L'angle d'incidence est l'angle formé entre le rayon incident et la normale, qui est une ligne imaginaire perpendiculaire à la surface de séparation des deux milieux au point d'incidence. De même, l'angle de réfraction est l'angle formé entre le rayon réfracté et la normale. Il est crucial de toujours mesurer les angles par rapport à la normale, et non par rapport à la surface elle-même.
Comprendre et Appliquer la Formule
Pour bien utiliser la formule de Snell-Descartes, suivez ces étapes :
- Identifiez clairement les deux milieux et leurs indices de réfraction (n1 et n2).
- Déterminez l'angle d'incidence (θ1), en vous assurant de le mesurer par rapport à la normale.
- Utilisez la formule n1 sin(θ1) = n2 sin(θ2) pour calculer l'angle de réfraction (θ2). Vous devrez peut-être utiliser la fonction arcsin (sin-1) de votre calculatrice pour trouver l'angle.
- Interprétez le résultat : si n2 > n1, alors θ2 < θ1 (le rayon se rapproche de la normale). Si n2 < n1, alors θ2 > θ1 (le rayon s'éloigne de la normale).
Exemples Concrets
Exemple 1 : Un rayon de lumière passe de l'air (n1 = 1) à l'eau (n2 = 1.33) avec un angle d'incidence de 30°. Quel est l'angle de réfraction ?
1 sin(30°) = 1.33 sin(θ2)
sin(θ2) = (1 * sin(30°)) / 1.33 ≈ 0.376
θ2 = arcsin(0.376) ≈ 22.1°
L'angle de réfraction est d'environ 22.1°. Le rayon se rapproche de la normale car la lumière passe d'un milieu moins réfringent (air) à un milieu plus réfringent (eau).
Exemple 2 : Un rayon de lumière passe du verre (n1 = 1.5) à l'air (n2 = 1) avec un angle d'incidence de 45°. Quel est l'angle de réfraction ?
1.5 sin(45°) = 1 sin(θ2)
sin(θ2) = (1.5 * sin(45°)) / 1 ≈ 1.06
Ici, sin(θ2) est supérieur à 1, ce qui est impossible. Cela signifie que dans cette situation, il y a réflexion totale interne (voir la section suivante).
Réflexion Totale Interne
La réflexion totale interne se produit lorsque la lumière passe d'un milieu d'indice de réfraction élevé à un milieu d'indice de réfraction plus faible, et que l'angle d'incidence est suffisamment grand. Dans ce cas, au lieu d'être réfractée, toute la lumière est réfléchie à l'intérieur du premier milieu. L'angle d'incidence critique (θc) est l'angle pour lequel l'angle de réfraction serait de 90°. On peut le calculer avec la formule:
sin(θc) = n2 / n1
Si l'angle d'incidence est supérieur à l'angle critique, il y a réflexion totale interne. C'est ce phénomène qui est utilisé dans les fibres optiques pour guider la lumière sur de longues distances.
Applications des Lois de Snell-Descartes
Les lois de Snell-Descartes ont de nombreuses applications pratiques :
- Lentilles : La conception des lentilles (pour les lunettes, les microscopes, les télescopes, etc.) repose sur la réfraction de la lumière à travers des surfaces courbes.
- Fibres optiques : La transmission de l'information sur de longues distances via la réflexion totale interne.
- Prismes : La séparation de la lumière blanche en ses différentes couleurs (dispersion).
- Mirages : Les mirages sont dus à la réfraction de la lumière à travers des couches d'air de températures différentes, donc d'indices de réfraction différents.
- L'apparente position des objets sous l'eau : Un objet situé au fond d'une piscine apparaît plus proche de la surface qu'il ne l'est réellement en raison de la réfraction de la lumière en passant de l'eau à l'air.
Ce qu'il faut retenir
- Réfraction : Changement de direction d'une onde (lumière) lorsqu'elle passe d'un milieu à un autre.
- Indice de réfraction (n) : Mesure de la vitesse de la lumière dans un milieu (n = c/v, où c est la vitesse de la lumière dans le vide et v est la vitesse de la lumière dans le milieu).
- Première loi de Snell-Descartes : Le rayon incident, la normale et le rayon réfracté sont coplanaires.
- Deuxième loi de Snell-Descartes : n1 sin(θ1) = n2 sin(θ2).
- Angle d'incidence (θ1) : Angle entre le rayon incident et la normale.
- Angle de réfraction (θ2) : Angle entre le rayon réfracté et la normale.
- Réflexion totale interne : Phénomène où la lumière est complètement réfléchie à l'intérieur d'un milieu lorsqu'elle tente de passer à un milieu d'indice de réfraction inférieur, et que l'angle d'incidence est supérieur à l'angle critique.
- Angle critique (θc) : Angle d'incidence pour lequel l'angle de réfraction est de 90° (sin(θc) = n2 / n1).
FAQ
-
Qu'est-ce que la normale ?
La normale est une ligne imaginaire perpendiculaire à la surface de séparation des deux milieux au point d'incidence. Elle est essentielle pour mesurer les angles d'incidence et de réfraction. -
Comment savoir si un rayon va se rapprocher ou s'éloigner de la normale lors de la réfraction ?
Si la lumière passe d'un milieu d'indice de réfraction plus faible à un milieu d'indice de réfraction plus élevé (par exemple, de l'air à l'eau), le rayon réfracté se rapproche de la normale. Inversement, si la lumière passe d'un milieu d'indice de réfraction plus élevé à un milieu d'indice de réfraction plus faible (par exemple, de l'eau à l'air), le rayon réfracté s'éloigne de la normale. -
Dans quel cas la réflexion totale interne se produit-elle ?
La réflexion totale interne se produit lorsque la lumière se propage d'un milieu ayant un indice de réfraction élevé vers un milieu ayant un indice de réfraction plus faible et que l'angle d'incidence est supérieur à l'angle critique. -
L'indice de réfraction peut-il être inférieur à 1 ?
Non, en général, l'indice de réfraction est toujours supérieur ou égal à 1. Un indice de réfraction inférieur à 1 impliquerait que la lumière se propage plus rapidement dans ce milieu que dans le vide, ce qui contredirait la théorie de la relativité d'Einstein. Cependant, il existe des situations spécifiques (par exemple, avec certains métamatériaux) où un indice de réfraction effectif inférieur à 1 peut être observé sur une gamme de fréquences limitée.
