Physique-Chimie > Mécanique > Dynamique > Tension d'un fil

Comprendre et Calculer la Tension d'un Fil

Explorez le concept de tension d'un fil en physique, ses applications et comment la calculer. Cette ressource est conçue pour les élèves de lycée et comprend des explications claires, des exemples concrets et des exercices.

Introduction à la Tension d'un Fil

La tension d'un fil est une force de traction exercée par un fil, une corde ou un câble sur un objet auquel il est attaché. Cette force agit dans la direction du fil et est causée par la tension interne créée lorsque le fil est tiré ou tendu. Imaginez un fil utilisé pour suspendre un objet : la tension du fil compense le poids de l'objet, le maintenant en équilibre. Il est crucial de comprendre que la tension est une force, et par conséquent, elle est mesurée en Newtons (N).

Origine de la Tension

La tension naît des forces intermoléculaires au sein du fil. Lorsque vous tirez sur un fil, vous étirez légèrement les liaisons entre les molécules qui le composent. Ces liaisons résistent à l'étirement, générant une force interne qui se manifeste comme la tension. Plus la force appliquée est grande, plus la tension interne est élevée, jusqu'à la rupture du fil si sa limite de résistance est dépassée. Il est important de noter que la tension est une force interne au fil qui se manifeste extérieurement en tirant sur les objets attachés.

Tension dans un Fil Idéal

En physique, on introduit souvent la notion de fil idéal pour simplifier les calculs. Un fil idéal possède les caractéristiques suivantes:

  • Masse négligeable : On considère que la masse du fil est suffisamment petite pour ne pas affecter significativement les résultats.
  • Inextensible : Le fil ne s'allonge pas sous l'effet de la tension. Sa longueur reste constante.
Dans un fil idéal, la tension est la même en tout point du fil. Cette simplification permet de concentrer l'attention sur les forces agissant sur les objets connectés au fil.

Calcul de la Tension

Le calcul de la tension dépend de la situation physique. Voici quelques cas courants:

  • Objet suspendu à un fil: Dans ce cas, la tension (T) est égale au poids (P) de l'objet, c'est-à-dire T = P = m * g, où m est la masse de l'objet et g est l'accélération due à la gravité (environ 9.81 m/s²).
  • Objet tiré par un fil horizontalement: Si l'objet est tiré à vitesse constante, la tension (T) est égale à la force de frottement (Ff) exercée sur l'objet, c'est-à-dire T = Ff. Si l'objet est accéléré, la tension est égale à la force résultante agissant sur l'objet (T = m * a, où a est l'accélération).
  • Système avec plusieurs fils et poulies: L'analyse devient plus complexe, nécessitant l'application des lois de Newton et la prise en compte de la géométrie du système. Il est essentiel de décomposer les forces en composantes horizontales et verticales pour résoudre le problème.

Exemple Concret : Un lustre suspendu

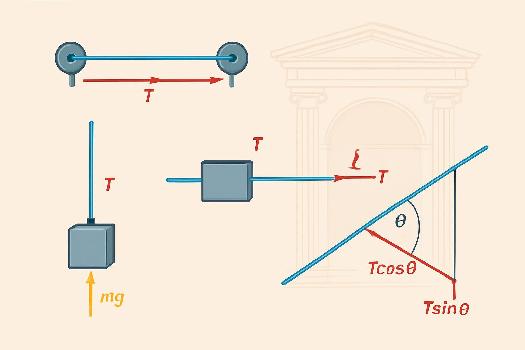
Considérons un lustre de 5 kg suspendu au plafond par un fil. Calculons la tension du fil.Le poids du lustre est P = m * g = 5 kg * 9.81 m/s² = 49.05 N.Puisque le lustre est en équilibre, la tension du fil doit compenser exactement ce poids. Donc, la tension du fil est T = 49.05 N.

Influence de l'Angle d'un Fil

Lorsque le fil n'est pas vertical, la tension doit être décomposée en composantes verticale et horizontale. La composante verticale compense le poids de l'objet, tandis que la composante horizontale affecte l'équilibre du système. Par exemple, si un objet est suspendu à deux fils formant un angle, la tension dans chaque fil sera supérieure à la moitié du poids de l'objet, car chaque fil ne supporte qu'une composante du poids. L'analyse trigonométrique est nécessaire pour déterminer les composantes de la tension et résoudre le problème. Rappel Trigonométrie:

  • sin(θ) = Opposé / Hypothénuse
  • cos(θ) = Adjacent / Hypothénuse
  • tan(θ) = Opposé / Adjacent

Ce qu'il faut retenir

  • La tension est une force de traction exercée par un fil.
  • Elle est mesurée en Newtons (N).
  • Dans un fil idéal (masse négligeable et inextensible), la tension est la même en tout point.
  • Le calcul de la tension dépend de la situation : T = m*g (objet suspendu), T = Ff (objet tiré à vitesse constante), etc.
  • Lorsque le fil forme un angle, la tension doit être décomposée en composantes verticale et horizontale.
Il est essentiel de maîtriser les lois de Newton et la trigonométrie pour résoudre les problèmes impliquant la tension d'un fil. N'oubliez pas de toujours faire un schéma du système et d'identifier clairement les forces en présence.

← Chocs élastiques et inélastiques : comprendre les collisions Conditions d'équilibre d'un corps rigide : Translation et Rotation →

FAQ

  • Qu'est-ce qui arrive si la tension d'un fil dépasse sa limite de résistance?

    Si la tension appliquée à un fil dépasse sa limite de résistance, le fil se casse ou se rompt.
  • La tension est-elle toujours la même dans un fil réel?

    Non, dans un fil réel, la tension peut varier légèrement en fonction de la masse du fil et des forces qui y sont appliquées. Cependant, pour simplifier les calculs, on considère souvent le fil comme idéal.
  • Comment la tension affecte-t-elle l'accélération d'un objet?

    La tension, étant une force, contribue à la force résultante agissant sur un objet. Selon la deuxième loi de Newton (F = m*a), la force résultante détermine l'accélération de l'objet. Donc, la tension influence directement l'accélération.