Force de Lorentz : Le Mouvement des Charges dans un Champ Magnétique

Introduction à la Force de Lorentz

La force de Lorentz est la force exercée sur une charge électrique en mouvement dans un champ magnétique. Elle est fondamentale pour comprendre une multitude de phénomènes, allant du fonctionnement des moteurs électriques à la trajectoire des particules chargées dans les accélérateurs de particules. Cette force est toujours perpendiculaire à la fois à la vitesse de la charge et au champ magnétique, ce qui implique qu'elle ne modifie pas l'énergie cinétique de la particule, mais uniquement sa direction.

Formule de la Force de Lorentz

L'expression mathématique de la force de Lorentz est la suivante: F = q (v ∧ B) Où:

• F est la force de Lorentz (en Newtons, N)
• q est la charge électrique de la particule (en Coulombs, C)
• v est la vitesse de la particule (en mètres par seconde, m/s)
• B est le champ magnétique (en Teslas, T)
• ∧ représente le produit vectoriel.

Le produit vectoriel (v ∧ B) est un vecteur dont la magnitude est |v||B|sin(θ), où θ est l'angle entre les vecteurs v et B. La direction de ce vecteur est perpendiculaire au plan formé par v et B, et son sens est donné par la règle de la main droite (voir explication ci-dessous). La règle de la main droite est un outil mnémotechnique essentiel pour déterminer le sens de la force de Lorentz.

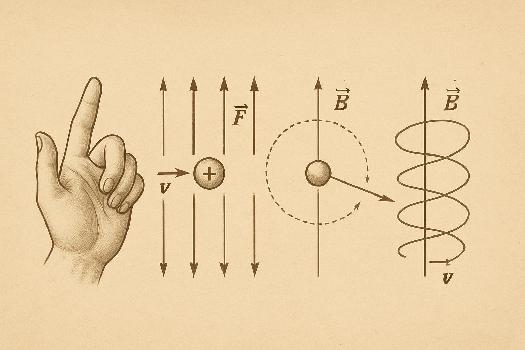
Règle de la Main Droite (pour les charges positives)

La règle de la main droite est une méthode pratique pour déterminer la direction de la force de Lorentz :

1. Orientez votre main droite de sorte que vos doigts pointent dans la direction de la vitesse v de la charge.
2. Pliez vos doigts pour qu'ils pointent dans la direction du champ magnétique B.
3. Votre pouce étendu indiquera la direction de la force de Lorentz F.

Important: Cette règle s'applique aux charges positives. Pour une charge négative, la direction de la force est opposée à celle indiquée par la règle de la main droite.

Trajectoire d'une Charge dans un Champ Magnétique Uniforme

Lorsqu'une charge se déplace dans un champ magnétique uniforme avec une vitesse perpendiculaire au champ, elle subit une force de Lorentz constante en magnitude et toujours perpendiculaire à sa vitesse. Cette force agit comme une force centripète, contraignant la charge à se déplacer selon une trajectoire circulaire. Le rayon (r) de ce cercle peut être calculé à partir de l'équation suivante, obtenue en égalant la force de Lorentz à la force centripète : q v B = m v² / r d'où: r = m v / (q B) Où:

• m est la masse de la particule (en kilogrammes, kg)

La période (T) du mouvement circulaire est: T = 2πr / v = 2πm / (qB) Et la fréquence (f) est: f = 1/T = qB / (2πm) Si la vitesse de la charge a une composante parallèle au champ magnétique, la trajectoire devient une hélice. La composante perpendiculaire à B induit le mouvement circulaire, tandis que la composante parallèle à B induit un mouvement uniforme le long des lignes de champ.

Exemples Concrets

• Spectromètre de Masse: Les spectromètres de masse utilisent la force de Lorentz pour séparer les ions en fonction de leur rapport masse/charge. Les ions sont accélérés dans un champ électrique, puis déviés par un champ magnétique. Le rayon de leur trajectoire circulaire dépend de leur masse et de leur charge, permettant ainsi de les identifier.
• Moteurs Électriques: Les moteurs électriques exploitent la force de Lorentz pour convertir l'énergie électrique en énergie mécanique. Un courant électrique traversant une bobine placée dans un champ magnétique subit une force qui fait tourner la bobine.
• Accélérateurs de Particules: Les accélérateurs de particules utilisent des champs magnétiques pour contraindre les particules chargées à se déplacer selon une trajectoire circulaire tout en étant accélérées. Cela permet d'atteindre des énergies très élevées et d'étudier la structure de la matière.
• L'aurore boréale: Les aurores boréales se forment lorsque des particules chargées provenant du soleil interagissent avec le champ magnétique terrestre. Ces particules sont déviées vers les pôles et entrent en collision avec les atomes de l'atmosphère, créant de la lumière.

Ce qu'il faut retenir

• La force de Lorentz agit sur une charge en mouvement dans un champ magnétique.
• Sa formule est F = q (v ∧ B).
• Elle est perpendiculaire à la vitesse et au champ magnétique.
• La règle de la main droite permet de déterminer sa direction (pour les charges positives).
• Dans un champ uniforme, une charge peut avoir une trajectoire circulaire (si v est perpendiculaire à B) ou hélicoïdale (si v a une composante parallèle à B).
• La force de Lorentz est utilisée dans de nombreuses applications technologiques, telles que les moteurs électriques, les spectromètres de masse et les accélérateurs de particules.