Physique-Chimie > Mécanique > Cinématique > Mouvement parabolique (projectile)

Mouvement Parabolique d'un Projectile : Analyse Complète

Étude détaillée du mouvement parabolique d'un projectile : composantes de la vitesse, portée, flèche, et applications pratiques. Comprend des exemples et des exercices pour une compréhension approfondie.

Introduction au Mouvement Parabolique

Le mouvement parabolique décrit la trajectoire d'un objet lancé dans un champ gravitationnel uniforme, sans résistance de l'air. Cette trajectoire est une parabole. Comprendre ce mouvement nécessite d'analyser les composantes horizontale et verticale de la vitesse et de l'accélération.

Imaginez que vous lancez une balle de basket. Sa trajectoire suit une courbe, qui est une parabole. Le mouvement parabolique est la description mathématique de cette courbe.

Composantes de la Vitesse Initiale

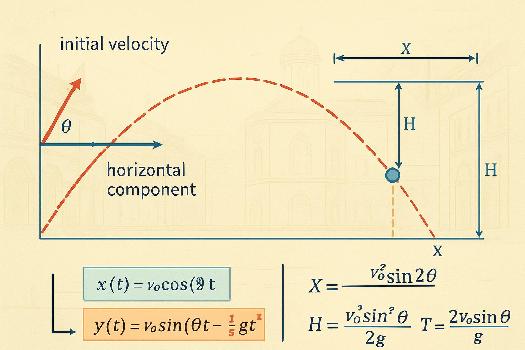
La vitesse initiale v0 du projectile peut être décomposée en deux composantes orthogonales :

  • v0x = v0 cos(θ) : La composante horizontale. Elle est constante tout au long du mouvement (en absence de frottement).
  • v0y = v0 sin(θ) : La composante verticale. Elle diminue en montant, s'annule au sommet de la trajectoire, puis augmente en descendant.
Où θ est l'angle de lancement par rapport à l'horizontale.

Pour bien visualiser cela, imaginez que vous déplacez une lampe torche horizontalement (v0x) et verticalement (v0y) en même temps. La combinaison de ces deux mouvements simples crée le mouvement parabolique.

Analyse du Mouvement Horizontal

Le mouvement horizontal est un mouvement uniforme (vitesse constante). L'équation de la position horizontale x(t) est donnée par :

x(t) = v0x t = v0 cos(θ) t

Cela signifie que la distance parcourue horizontalement augmente linéairement avec le temps. Pensez à une voiture qui roule à vitesse constante sur une route droite : elle parcourt des distances égales en des intervalles de temps égaux.

Analyse du Mouvement Vertical

Le mouvement vertical est un mouvement uniformément varié (accélération constante due à la gravité, g, dirigée vers le bas). Les équations de la vitesse verticale vy(t) et de la position verticale y(t) sont données par :

  • vy(t) = v0y - gt = v0 sin(θ) - gt
  • y(t) = v0y t - (1/2)gt2 = v0 sin(θ) t - (1/2)gt2
La vitesse verticale diminue en montant à cause de la gravité, s'annule au sommet, puis devient négative en descendant.

Imaginez maintenant une pomme qui tombe d'un arbre. Sa vitesse augmente de plus en plus vite à cause de l'attraction terrestre.

Portée et Flèche

  • Portée (X) : La distance horizontale totale parcourue par le projectile lorsqu'il revient à sa hauteur initiale (y = 0). Elle est donnée par :

    X = (v02 sin(2θ)) / g

    La portée est maximale pour un angle de lancement de 45°.
  • Flèche (H) : La hauteur maximale atteinte par le projectile. Elle est atteinte lorsque la vitesse verticale est nulle (vy = 0). Elle est donnée par :

    H = (v02 sin2(θ)) / (2g)
La portée vous dit à quelle distance atterrira la balle, et la flèche vous indique la hauteur maximale qu'elle atteindra.

Temps de Vol

Le temps de vol (T) est le temps total que le projectile passe en l'air. Il est donné par :

T = (2v0 sin(θ)) / g

Le temps de vol est deux fois le temps nécessaire pour atteindre la flèche (sommet de la trajectoire).

Exemples et Applications

Le mouvement parabolique est présent dans de nombreux domaines :

  • Sports : Lancer d'une balle de baseball, tir d'un ballon de football, saut en longueur.
  • Artillerie : Trajectoire d'un obus.
  • Balistique : Mouvement d'un projectile.
  • Jeux vidéo : Mouvement des projectiles dans les jeux.
En comprenant le mouvement parabolique, on peut prédire la trajectoire d'un projectile et optimiser sa portée ou sa hauteur.

Ce qu'il faut retenir

  • Le mouvement parabolique est la combinaison d'un mouvement uniforme horizontal et d'un mouvement uniformément varié vertical.
  • La vitesse initiale est décomposée en composantes horizontale (constante) et verticale (variable).
  • La portée (X) est la distance horizontale parcourue.
  • La flèche (H) est la hauteur maximale atteinte.
  • Le temps de vol (T) est le temps total passé en l'air.
  • Les équations clés sont :
    • x(t) = v0 cos(θ) t
    • y(t) = v0 sin(θ) t - (1/2)gt2
    • X = (v02 sin(2θ)) / g
    • H = (v02 sin2(θ)) / (2g)
    • T = (2v0 sin(θ)) / g

← Moment d'une force par rapport à un axe Mouvement Rectiligne Uniforme (MRU) →

FAQ

  • Quelle est l'influence de la résistance de l'air sur le mouvement parabolique ?

    La résistance de l'air complique considérablement le modèle. En présence de résistance de l'air, la trajectoire n'est plus une parabole parfaite. La portée est réduite, et la trajectoire devient asymétrique. Les calculs deviennent plus complexes et nécessitent souvent des méthodes numériques.
  • Comment calculer l'angle de lancement optimal pour atteindre une cible donnée ?

    Pour une cible à la même hauteur que le point de lancement, l'angle optimal est de 45° (sans résistance de l'air). Cependant, si la cible est à une hauteur différente, l'angle optimal doit être calculé en résolvant une équation qui prend en compte la différence de hauteur. Cela peut nécessiter des méthodes numériques ou des approximations.