Conditions d'équilibre d'un corps rigide : Translation et Rotation

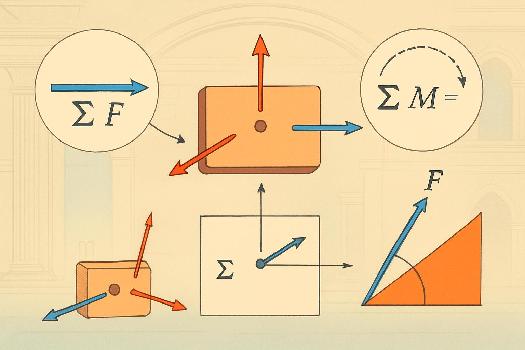
Introduction à l'équilibre d'un corps rigide

L'étude de l'équilibre d'un corps rigide est fondamentale en mécanique. Un corps rigide est dit en équilibre lorsqu'il ne subit ni translation (mouvement de déplacement) ni rotation (mouvement de pivotement). Pour qu'un corps rigide soit en équilibre, deux conditions doivent être simultanément satisfaites. Ces conditions sont essentielles pour comprendre et prédire le comportement statique des objets qui nous entourent, des ponts aux bâtiments, en passant par les machines simples.

Condition d'équilibre en translation

La première condition pour l'équilibre d'un corps rigide est que la somme vectorielle de toutes les forces agissant sur ce corps doit être égale à zéro. Mathématiquement, cela s'écrit : ∑ F = 0.

Cela signifie que si vous additionnez toutes les forces agissant sur l'objet, en tenant compte de leur direction et de leur magnitude, le résultat doit être nul. En d'autres termes, il n'y a pas de force nette qui pourrait provoquer un mouvement de translation (accélération linéaire) du corps.

En pratique, cela implique que dans un système de coordonnées cartésiennes (x, y, z), la somme des composantes des forces dans chaque direction doit être nulle : ∑ F_x = 0, ∑ F_y = 0, et ∑ F_z = 0.

Exemple : Imaginez un livre posé sur une table. La force de gravité (son poids) tire le livre vers le bas. La table exerce une force égale et opposée vers le haut, appelée réaction normale. Si ces deux forces sont les seules forces agissant sur le livre et qu'elles s'annulent, la somme des forces est nulle, et le livre reste immobile.

Condition d'équilibre en rotation

La deuxième condition pour l'équilibre d'un corps rigide est que la somme des moments de toutes les forces agissant sur le corps, par rapport à n'importe quel point, doit être égale à zéro. Le moment d'une force, souvent appelé couple, mesure l'effet de rotation de cette force autour d'un point donné. Mathématiquement, cela s'écrit : ∑ M = 0.

Cela signifie que les forces qui tendent à faire tourner l'objet dans un sens doivent être contrebalancées par des forces qui tendent à le faire tourner dans le sens opposé, de sorte que la rotation nette soit nulle.

Le moment d'une force F par rapport à un point O est donné par le produit vectoriel du vecteur position r (du point O au point d'application de la force) et de la force F : M = r x F. La magnitude du moment est M = r * F * sin(θ), où θ est l'angle entre r et F.

Exemple : Imaginez une balançoire. Si deux personnes de poids égal s'assoient à égale distance du point de pivot, les moments créés par leurs poids s'annulent, et la balançoire reste en équilibre (horizontale). Si l'une des personnes est plus lourde, ou si elle s'assoit plus loin du pivot, le moment créé par son poids sera plus important, et la balançoire basculera de son côté jusqu'à ce que l'équilibre soit rétabli par une autre force (par exemple, le contact avec le sol).

Application pratique : Résolution de problèmes d'équilibre

Pour résoudre un problème d'équilibre de corps rigide, suivez les étapes suivantes :

1. Dessinez un diagramme de corps libre : Représentez le corps rigide et toutes les forces qui agissent sur lui. Indiquez les points d'application des forces.

2. Choisissez un système de coordonnées : Définissez un système de coordonnées (x, y, z) pour faciliter la décomposition des forces en composantes.

3. Appliquez les conditions d'équilibre en translation : Écrivez les équations ∑ F_x = 0, ∑ F_y = 0, et ∑ F_z = 0. Cela vous donnera un ensemble d'équations algébriques.

4. Choisissez un point de référence pour le calcul des moments : Le choix de ce point est arbitraire, mais il est souvent judicieux de choisir un point où passent plusieurs forces inconnues, afin de simplifier les calculs.

5. Appliquez la condition d'équilibre en rotation : Calculez les moments de toutes les forces par rapport au point de référence, et écrivez l'équation ∑ M = 0.

6. Résolvez le système d'équations : Vous obtenez un système d'équations algébriques que vous pouvez résoudre pour trouver les inconnues (forces, distances, angles...).

Exemple: Une poutre homogène de longueur L et de poids P est soutenue à ses deux extrémités A et B. Déterminez les forces de réaction aux points A et B. (Solution : Les forces de réaction en A et B sont chacune égales à P/2).

Importance des conditions d'équilibre

Les conditions d'équilibre sont cruciales dans de nombreux domaines de l'ingénierie et de la physique. Elles permettent de concevoir des structures stables et sûres, d'analyser le comportement des machines et des mécanismes, et de comprendre les phénomènes physiques qui régissent le monde qui nous entoure. Par exemple, elles sont utilisées pour concevoir des ponts qui peuvent supporter des charges importantes sans s'effondrer, pour analyser la stabilité des bâtiments, ou pour concevoir des grues qui peuvent soulever des charges lourdes en toute sécurité.

Ce qu'il faut retenir

• Définition de l'équilibre: Un corps rigide est en équilibre s'il ne subit ni translation, ni rotation.
• Condition d'équilibre en translation: La somme vectorielle de toutes les forces agissant sur le corps doit être nulle : ∑ F = 0.
• Condition d'équilibre en rotation: La somme des moments de toutes les forces agissant sur le corps, par rapport à n'importe quel point, doit être nulle : ∑ M = 0.
• Résolution de problèmes: Suivre une méthodologie structurée (diagramme de corps libre, choix d'un système de coordonnées, application des conditions d'équilibre, résolution du système d'équations).
• Importance pratique: Les conditions d'équilibre sont essentielles pour la conception et l'analyse de structures et de machines stables et sûres.