Exercices Corrigés : Maîtriser les Prismes et la Dispersion Lumineuse

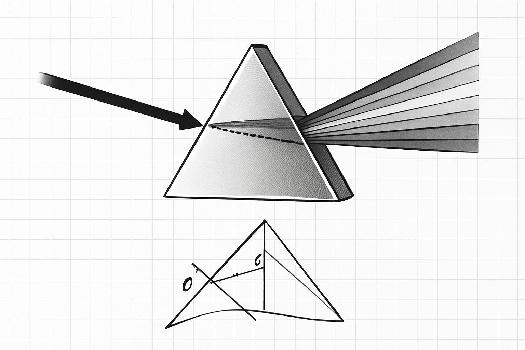
Exercice 1 : Calcul de l'Angle de Déviation

Énoncé : Un rayon de lumière monochromatique (jaune) frappe un prisme en verre d'angle au sommet A = 60°. L'indice de réfraction du verre pour cette longueur d'onde est n = 1.5. Si l'angle d'incidence est de 45°, quel est l'angle de déviation du rayon ? Solution :

1. Appliquer la loi de Snell-Descartes à la première interface air-verre : sin(θ1) = n sin(θ2) où θ₁ = 45°. Donc, sin(45°) = 1.5 sin(θ2) => θ2 = arcsin(sin(45°)/1.5) ≈ 28.13°
2. Calculer l'angle d'incidence sur la deuxième face du prisme : L'angle entre la normale à la première face et le rayon réfracté est θ₂. L'angle entre ce rayon et la deuxième face (à l'intérieur du prisme) est donc A - θ2 = 60° - 28.13° ≈ 31.87°. L'angle d'incidence (θ₃) sur la deuxième face est alors 90° - 31.87° ≈ 58.13°
3. Appliquer la loi de Snell-Descartes à la deuxième interface verre-air : n sin(θ3) = sin(θ4). Donc, 1.5 sin(58.13°) = sin(θ4) => θ4 = arcsin(1.5 * sin(58.13°)) ≈ 102.06°. Cependant, cet angle est impossible. L'angle d'incidence correct à utiliser est 90 - 31.87 = 58.13, on corrige l'angle de refraction en utilisant 1.5 * sin(31.87) = sin(r2) et donc r2 = 51.47. Donc l'angle émergent est de r2 - A = 51.47 - 60 = -8.53, on prend la valeur absolue et on obtient une déviation de 8.53.
4. Calculer l'angle de déviation (D) : D = θ1 + θ4 - A = 45° + 51.47° - 60° = 36.47°. Donc l'angle de déviation est d'environ 36.47°.

Exercice 2 : Détermination de l'Indice de Réfraction

Énoncé : Un prisme équilatéral (angle au sommet A = 60°) a un angle de déviation minimale de 38.9°. Quel est l'indice de réfraction du matériau du prisme pour la longueur d'onde utilisée ? Solution :

• Utiliser la formule reliant l'indice de réfraction (n), l'angle au sommet (A) et l'angle de déviation minimale (D_min) : n = sin((A + Dmin)/2) / sin(A/2)
• Substituer les valeurs : n = sin((60° + 38.9°)/2) / sin(60°/2) = sin(49.45°) / sin(30°) ≈ 1.58

Exercice 3 : Dispersion et Spectre

Énoncé : La lumière blanche incidente sur un prisme en flint est décomposée en un spectre visible. L'indice de réfraction du flint pour la lumière rouge est n_rouge = 1.662 et pour la lumière violette n_violet = 1.684. Sachant que l'angle d'incidence est de 45° et que l'angle du prisme est de 60°, calculez l'écart angulaire entre les rayons rouge et violet à la sortie du prisme. Solution : (Simplification, on ne demandera pas aux étudiants de résoudre complètement, mais plutôt le raisonnement)

• Le but est de determiner les deux angles de deviation.
• Avec ces deux angles de deviation, l'ecart angulaire est simplement la difference entre ces angles.
• Ce problème démontre l'importance de l'indice de réfraction sur l'angle de déviation.

Ce qu'il faut retenir

• La loi de Snell-Descartes est essentielle pour calculer les angles de réfraction.
• La formule reliant n, A et D_min est cruciale pour déterminer l'indice de réfraction.
• La dispersion est la cause de la séparation des couleurs dans un prisme.