Potentiel électrique : Définition, calcul et applications

Définition du potentiel électrique

Le potentiel électrique, souvent noté *V*, est une grandeur scalaire qui caractérise l'état électrique d'un point de l'espace. Contrairement au champ électrique qui est une grandeur vectorielle, le potentiel électrique est un nombre. On peut le voir comme l'énergie potentielle électrique par unité de charge. Plus précisément, c'est le travail qu'il faut fournir pour amener une charge unité positive depuis l'infini jusqu'à un point donné, sans modifier son énergie cinétique. L'unité de potentiel électrique est le volt (V). Il est important de noter que seul la *différence* de potentiel (tension) est physiquement significative. On peut choisir arbitrairement le point où le potentiel est nul, souvent pris à l'infini ou à la masse.

Lien entre potentiel électrique et champ électrique

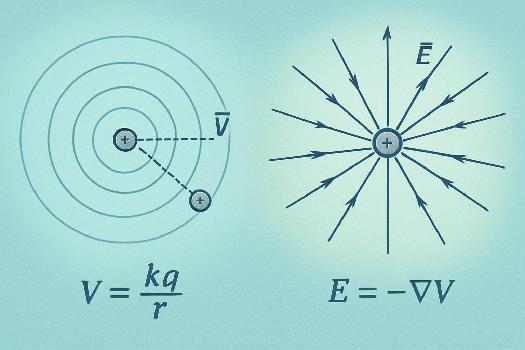
Le potentiel électrique et le champ électrique sont intimement liés. Le champ électrique est le gradient négatif du potentiel électrique. Mathématiquement, on peut écrire : E = -∇V, où E est le champ électrique et ∇V est le gradient du potentiel électrique. En termes simples, cela signifie que le champ électrique pointe dans la direction où le potentiel électrique diminue le plus rapidement. En une dimension, cela se simplifie en E = -dV/dx. Une forte variation du potentiel dans l'espace correspond à un champ électrique intense. Le champ électrique est donc une force qui dérive du potentiel électrique. Les surfaces équipotentielles sont des surfaces où le potentiel électrique est constant. Le champ électrique est toujours perpendiculaire aux surfaces équipotentielles.

Calcul du potentiel électrique

Le potentiel électrique créé par une charge ponctuelle *q* à une distance *r* est donné par la formule : V = k*q/r, où k est la constante de Coulomb (k ≈ 8.99 x 10⁹ N m²/C²). Pour un ensemble de charges ponctuelles, le potentiel électrique en un point est la somme algébrique des potentiels créés par chaque charge individuellement. Pour une distribution continue de charges, on utilise l'intégrale : V = ∫ k dq/r, où dq est un élément infinitésimal de charge et r est la distance de dq au point où l'on calcule le potentiel. Le calcul du potentiel est souvent plus simple que le calcul direct du champ électrique, surtout pour les distributions de charges complexes, car le potentiel est une grandeur scalaire.

Surfaces équipotentielles

Une surface équipotentielle est une surface où le potentiel électrique est constant en tout point. Par conséquent, la différence de potentiel entre deux points quelconques sur une surface équipotentielle est nulle. Les surfaces équipotentielles sont toujours perpendiculaires aux lignes de champ électrique. Pour une charge ponctuelle, les surfaces équipotentielles sont des sphères centrées sur la charge. Pour un champ électrique uniforme, les surfaces équipotentielles sont des plans perpendiculaires au champ. Le travail nécessaire pour déplacer une charge le long d'une surface équipotentielle est nul.

Applications du potentiel électrique

Le concept de potentiel électrique est fondamental dans de nombreux domaines de l'électricité et du magnétisme. Il est utilisé pour calculer l'énergie potentielle électrique d'une charge dans un champ électrique. Il est également utilisé pour analyser les circuits électriques, car la différence de potentiel (tension) entre deux points est ce qui provoque le mouvement des charges (courant). Le potentiel électrique est également utilisé en électronique, notamment pour analyser le fonctionnement des transistors et autres composants électroniques. Il est aussi utilisé dans l'imagerie médicale (IRM, scanner) et en physique des particules.

Exemple concret : Potentiel créé par deux charges

Considérons deux charges, q1 = +2 µC et q2 = -1 µC, situées respectivement aux points A(0,0) et B(4,0) (en mètres). Calculons le potentiel au point C(2,0). La distance de q1 à C est r1 = 2 m, et la distance de q2 à C est r2 = 2 m. Le potentiel créé par q1 en C est V1 = k*q1/r1 = (9 x 10⁹ N m²/C²) * (2 x 10^-6 C) / 2 m = 9000 V. Le potentiel créé par q2 en C est V2 = k*q2/r2 = (9 x 10⁹ N m²/C²) * (-1 x 10^-6 C) / 2 m = -4500 V. Le potentiel total en C est V = V1 + V2 = 9000 V - 4500 V = 4500 V. Cet exemple montre comment le potentiel total est la somme algébrique des potentiels individuels.

Ce qu'il faut retenir

• Le potentiel électrique est une grandeur scalaire représentant l'énergie potentielle par unité de charge.
• Il se mesure en volts (V).
• Seules les différences de potentiel sont physiquement significatives.
• Le champ électrique est le gradient négatif du potentiel électrique : E = -∇V.
• Les surfaces équipotentielles sont des surfaces où le potentiel est constant.
• Le champ électrique est toujours perpendiculaire aux surfaces équipotentielles.
• Pour une charge ponctuelle : V = k*q/r.
• Pour un ensemble de charges, le potentiel est la somme algébrique des potentiels individuels.