Incertitudes et Ajustements Linéaires: Cas des Droites d'Erreur

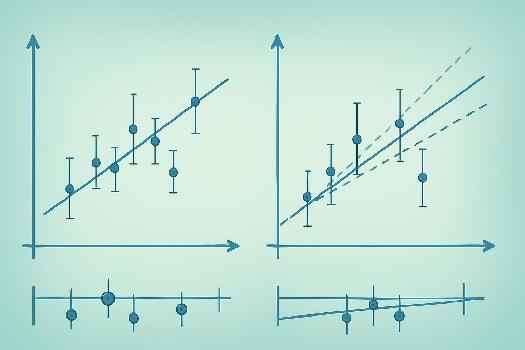
Introduction à l'Ajustement Linéaire et aux Droites d'Erreur

Quand utiliser un ajustement linéaire ? En Physique-Chimie, on rencontre souvent des relations linéaires entre deux grandeurs physiques. Par exemple, la loi d'Ohm (U = R * I) ou la loi de Hooke (F = k * Δx). Un ajustement linéaire consiste à trouver la droite qui représente le mieux un ensemble de points expérimentaux.

Pourquoi des droites d'erreur ? Puisque chaque mesure est entachée d'incertitude, chaque point expérimental est en réalité une zone d'incertitude. La 'meilleure' droite n'est donc pas unique. On peut tracer une famille de droites compatibles avec les incertitudes sur les mesures. L'ensemble de ces droites constitue la 'droite d'erreur'.

Représentation Graphique des Incertitudes

Avant d'effectuer un ajustement linéaire, il est crucial de représenter graphiquement les incertitudes sur les mesures. Chaque point expérimental (x_i, y_i) est représenté avec :

- Une barre d'erreur horizontale représentant l'incertitude sur la valeur de x_i.
- Une barre d'erreur verticale représentant l'incertitude sur la valeur de y_i.

La longueur de chaque barre d'erreur correspond à l'incertitude, souvent représentée par l'incertitude-type u(x_i) et u(y_i), ou par une incertitude élargie U(x_i) et U(y_i) (par exemple, avec un niveau de confiance de 95%).

Tracer les Droites Limites

Après avoir représenté les points expérimentaux avec leurs barres d'erreur, on trace deux droites 'limites' :

1. La droite de pente maximale (a_max) : C'est la droite de pente la plus forte qui reste compatible avec toutes les barres d'erreur. Elle passe par le bord inférieur de la barre d'erreur d'un point et le bord supérieur de la barre d'erreur d'un autre point.

2. La droite de pente minimale (a_min) : C'est la droite de pente la plus faible qui reste compatible avec toutes les barres d'erreur. Elle passe par le bord supérieur de la barre d'erreur d'un point et le bord inférieur de la barre d'erreur d'un autre point.

Ces deux droites définissent les limites de la droite d'erreur.

Détermination de la Pente et de l'Ordonnée à l'Origine

La 'meilleure' estimation de la pente (a) est la moyenne des pentes maximales et minimales :

a = (a_max + a_min) / 2

L'incertitude sur la pente est la moitié de la différence entre les pentes maximales et minimales :

u(a) = |a_max - a_min| / 2

De la même manière, on peut estimer l'ordonnée à l'origine (b) et son incertitude u(b) à partir des ordonnées à l'origine des droites limites.

Expression du Résultat et Interprétation

On exprime le résultat de l'ajustement linéaire sous la forme :

a = (valeur estimée de la pente ± incertitude sur la pente) unité
b = (valeur estimée de l'ordonnée à l'origine ± incertitude sur l'ordonnée à l'origine) unité

Il est crucial d'interpréter les résultats en tenant compte des incertitudes. Par exemple, si l'incertitude sur l'ordonnée à l'origine est importante, on ne peut pas conclure avec certitude que la droite passe par l'origine. Les incertitudes peuvent nous renseigner sur la pertinence du modèle linéaire utilisé.

Utilisation d'un logiciel

Il existe de nombreux logiciels permettant de calculer directement les incertitudes sur les coefficients d'une régression linéaire (tableur, logiciel de calcul scientifique, etc.). La démarche décrite ci-dessus reste cependant utile pour bien comprendre les fondements du calcul d'incertitudes dans ce contexte.

Ce qu'il faut retenir

• Un ajustement linéaire permet de trouver la droite qui représente le mieux un ensemble de points expérimentaux.
• Chaque point expérimental est représenté avec des barres d'erreur horizontales et verticales.
• On trace les droites de pente maximale et minimale compatibles avec les barres d'erreur.
• La pente et l'ordonnée à l'origine sont estimées comme la moyenne des valeurs maximales et minimales.
• Les incertitudes sur la pente et l'ordonnée à l'origine sont estimées à partir des droites limites.
• Il est crucial d'interpréter les résultats en tenant compte des incertitudes.