Physique-Chimie > Optique > Optique Géométrique > Distance focale, vergence

Distance focale et vergence : Comprendre les lentilles

Ce cours complet explique en détail la distance focale et la vergence, des concepts clés de l'optique géométrique. Il est conçu pour les élèves de lycée et aborde les définitions, les formules, les conventions de signe et des exemples concrets.

Introduction : Qu'est-ce qu'une lentille ?

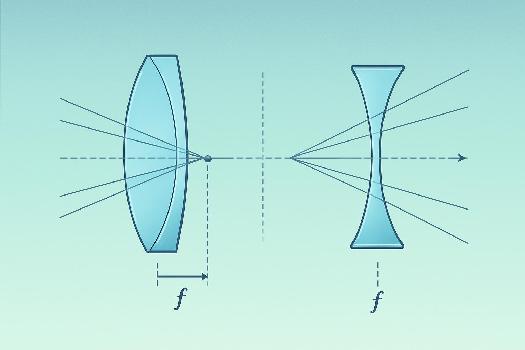
Une lentille est un élément optique transparent qui réfracte la lumière. Il existe deux types principaux de lentilles : les lentilles convergentes et les lentilles divergentes. Les lentilles convergentes font converger les rayons lumineux, tandis que les lentilles divergentes les font diverger. Nous allons étudier plus particulièrement les lentilles minces.

Définition de la distance focale (f)

La distance focale (f) est la distance entre le centre optique d'une lentille et son foyer principal image (F'). Le foyer principal image est le point où convergent les rayons lumineux parallèles à l'axe optique après avoir traversé la lentille convergente. Pour une lentille divergente, c'est le point d'où semblent provenir les rayons après avoir traversé la lentille.

Unité : La distance focale est mesurée en mètres (m).

Distance focale : Lentilles convergentes vs. divergentes

Il est crucial de distinguer les deux types de lentilles:

  • Lentille convergente: Sa distance focale f est positive (f > 0).
  • Lentille divergente: Sa distance focale f est négative (f < 0).

Cette convention de signe est fondamentale pour les calculs.

Définition de la vergence (C)

La vergence (C) d'une lentille est l'inverse de sa distance focale. Elle mesure la capacité de la lentille à faire converger ou diverger les rayons lumineux.

Formule : C = 1/f

Unité : La vergence est mesurée en dioptries (δ ou m-1).

Vergence : Lentilles convergentes vs. divergentes

Comme pour la distance focale, la vergence a un signe important:

  • Lentille convergente: Sa vergence C est positive (C > 0). Elle fait converger les rayons.
  • Lentille divergente: Sa vergence C est négative (C < 0). Elle fait diverger les rayons.

Une vergence élevée (en valeur absolue) indique une lentille plus puissante.

Exemple de calcul

Considérons une lentille convergente de distance focale f = 0,2 m. Sa vergence est C = 1/0,2 = 5 δ.

Considérons une lentille divergente de distance focale f = -0,5 m. Sa vergence est C = 1/-0,5 = -2 δ.

Influence de la vergence sur la formation des images

Une lentille avec une vergence positive forte formera une image plus petite et plus proche de la lentille qu'une lentille avec une vergence positive faible. Une lentille divergente produira toujours une image virtuelle, droite et plus petite que l'objet.

Applications concrètes

La distance focale et la vergence sont des concepts essentiels pour comprendre le fonctionnement des :

  • Lunettes: Correction de la vue (myopie, hypermétropie, astigmatisme).
  • Appareils photo: Focalisation de la lumière sur le capteur.
  • Télescopes: Observation d'objets lointains.
  • Microscopes: Observation d'objets très petits.

Conventions de signe : Résumé

Il est primordial de respecter les conventions de signe pour la distance focale et la vergence :

  • Lentille convergente : f > 0, C > 0
  • Lentille divergente : f < 0, C < 0

Le non-respect de ces conventions conduit à des erreurs dans les calculs.

Ce qu'il faut retenir

  • Distance focale (f) : Distance entre le centre optique et le foyer principal image, mesurée en mètres (m). Positive pour les lentilles convergentes, négative pour les lentilles divergentes.
  • Vergence (C) : Inverse de la distance focale (C = 1/f), mesurée en dioptries (δ ou m-1). Positive pour les lentilles convergentes, négative pour les lentilles divergentes.
  • La vergence caractérise la capacité d'une lentille à faire converger ou diverger les rayons lumineux.
  • Respecter les conventions de signe est essentiel pour les calculs.

← Diffraction de la lumière : Comprendre le principe Exercices Corrigés : Maîtriser les Prismes et la Dispersion Lumineuse →

FAQ

  • Comment déterminer si une lentille est convergente ou divergente sans connaître sa distance focale ?

    Vous pouvez faire passer un faisceau de rayons parallèles à travers la lentille. Si les rayons convergent après avoir traversé la lentille, elle est convergente. S'ils divergent, elle est divergente.
  • Pourquoi la distance focale est-elle négative pour une lentille divergente ?

    Par convention, on considère que la distance focale est négative car le foyer principal image est situé du même côté que l'objet, et non de l'autre côté de la lentille comme pour une lentille convergente.
  • Quelle est l'influence de l'indice de réfraction du matériau de la lentille sur sa distance focale ?

    L'indice de réfraction du matériau de la lentille influe sur sa distance focale. Un indice de réfraction plus élevé signifie que la lentille réfracte davantage la lumière, ce qui diminue sa distance focale (et augmente sa vergence).