Physique-Chimie > Optique > Optique Géométrique > Lentilles minces (convergentes et divergentes)

Lentilles minces : Convergence et Divergence

Découvrez le fonctionnement des lentilles minces, convergentes et divergentes. Comprenez comment elles modifient les rayons lumineux et leur rôle dans la formation des images. Ce cours est conçu pour les élèves de lycée en Physique-Chimie.

Introduction aux lentilles minces

Les lentilles minces sont des éléments optiques transparents, généralement en verre ou en plastique, dont les surfaces sont courbées. Leur principal effet est de réfracter la lumière, c'est-à-dire de modifier la direction des rayons lumineux qui les traversent. Elles sont dites 'minces' car leur épaisseur est négligeable par rapport à leur rayon de courbure.

Types de lentilles minces

Il existe deux grands types de lentilles minces:

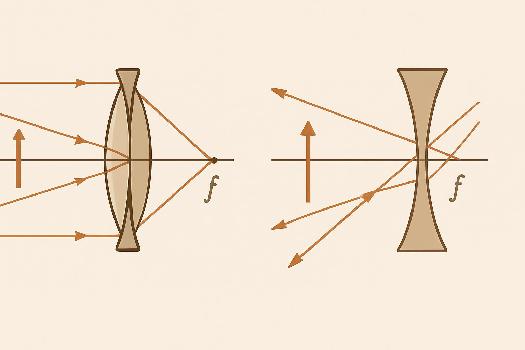
  1. Les lentilles convergentes : Elles sont plus épaisses au centre qu'aux bords. Elles font converger les rayons lumineux parallèles vers un point appelé foyer principal image. Elles sont souvent utilisées pour former des images réelles et agrandies.
  2. Les lentilles divergentes : Elles sont plus minces au centre qu'aux bords. Elles font diverger les rayons lumineux parallèles. Les rayons lumineux semblent provenir d'un point situé devant la lentille, appelé foyer principal image. Elles sont utilisées pour corriger la myopie et pour des applications où l'on souhaite élargir un faisceau lumineux.

Caractérisation d'une lentille mince

Pour caractériser une lentille mince, on utilise les éléments suivants:

  • Le centre optique (O): C'est le point central de la lentille. Tout rayon lumineux passant par le centre optique n'est pas dévié.
  • L'axe optique: C'est la droite passant par le centre optique et perpendiculaire aux faces de la lentille.
  • Le foyer principal image (F'): C'est le point où convergent les rayons lumineux parallèles à l'axe optique après avoir traversé une lentille convergente. Pour une lentille divergente, c'est le point d'où semblent provenir les rayons lumineux après avoir traversé la lentille.
  • Le foyer principal objet (F): C'est le point tel que les rayons lumineux issus de ce point, après avoir traversé la lentille, sont parallèles à l'axe optique. Le foyer objet est symétrique du foyer image par rapport au centre optique.
  • La distance focale (f'): C'est la distance entre le centre optique et le foyer principal image. Elle est positive pour les lentilles convergentes et négative pour les lentilles divergentes.
  • La vergence (C): C'est l'inverse de la distance focale: C = 1/f'. Elle s'exprime en dioptries (δ). Une lentille convergente a une vergence positive, tandis qu'une lentille divergente a une vergence négative.

Construction géométrique des images

Pour déterminer la position et la taille de l'image formée par une lentille, on utilise des constructions géométriques basées sur quelques rayons particuliers:

  1. Rayon passant par le centre optique (O): Il n'est pas dévié.
  2. Rayon parallèle à l'axe optique: Après avoir traversé la lentille convergente, il passe par le foyer principal image (F'). Après avoir traversé la lentille divergente, il semble provenir du foyer principal image (F').
  3. Rayon passant par le foyer principal objet (F): Après avoir traversé la lentille convergente, il devient parallèle à l'axe optique. Pour une lentille divergente, il se dirige vers le foyer objet F (situé derrière l'objet).
L'intersection d'au moins deux de ces rayons après la lentille permet de déterminer la position de l'image.

Formation des images

La nature de l'image (réelle ou virtuelle, droite ou inversée, agrandie ou réduite) dépend de la position de l'objet par rapport à la lentille.

  • Lentille convergente:
    • Si l'objet est situé à une distance supérieure à deux fois la distance focale (2f'), l'image est réelle, inversée et réduite.
    • Si l'objet est situé entre f' et 2f', l'image est réelle, inversée et agrandie.
    • Si l'objet est situé entre O et f', l'image est virtuelle, droite et agrandie (c'est le principe de la loupe).
  • Lentille divergente: L'image est toujours virtuelle, droite et réduite.

Formule de conjugaison et grandissement

La position de l'image peut être calculée à l'aide de la formule de conjugaison: 1/OA' - 1/OA = 1/f' Où:

  • OA est la distance entre le centre optique et l'objet (algébrique).
  • OA' est la distance entre le centre optique et l'image (algébrique).
  • f' est la distance focale (algébrique: positive pour les lentilles convergentes, négative pour les lentilles divergentes).
Le grandissement (γ) est défini comme le rapport de la taille de l'image (A'B') sur la taille de l'objet (AB): γ = A'B' / AB = OA' / OA Si γ > 0, l'image est droite. Si γ < 0, l'image est inversée. |γ| > 1 signifie que l'image est agrandie. |γ| < 1 signifie que l'image est réduite.

Ce qu'il faut retenir

  • Les lentilles minces peuvent être convergentes ou divergentes.
  • Une lentille convergente fait converger les rayons lumineux, tandis qu'une lentille divergente les fait diverger.
  • La distance focale (f') est une caractéristique importante de la lentille.
  • La vergence (C) est l'inverse de la distance focale.
  • Les rayons particuliers (passant par O, parallèles à l'axe optique, passant par F) permettent de construire géométriquement les images.
  • La nature de l'image (réelle/virtuelle, droite/inversée, agrandie/réduite) dépend de la position de l'objet.
  • La formule de conjugaison et le grandissement permettent de calculer la position et la taille de l'image.

← L'œil et les instruments optiques : principes et fonctionnement Les Interférences Lumineuses : Principe et Explications →

FAQ

  • Quelle est la différence entre une lentille convergente et une lentille divergente ?

    Une lentille convergente est plus épaisse au centre qu'aux bords et fait converger les rayons lumineux. Une lentille divergente est plus mince au centre qu'aux bords et fait diverger les rayons lumineux.
  • Comment déterminer si une image est réelle ou virtuelle ?

    Une image réelle peut être projetée sur un écran, tandis qu'une image virtuelle ne peut pas l'être. Dans les constructions géométriques, une image réelle est formée par l'intersection effective des rayons lumineux, tandis qu'une image virtuelle est formée par l'intersection des prolongements des rayons lumineux.
  • À quoi sert la formule de conjugaison ?

    La formule de conjugaison permet de calculer la position de l'image formée par une lentille en fonction de la position de l'objet et de la distance focale de la lentille.