Physique-Chimie > Optique > Optique Géométrique > Réflexion totale interne

Exercices Corrigés sur la Réflexion Totale Interne

Une série d'exercices corrigés pour maîtriser le concept de réflexion totale interne. Ces exercices couvrent le calcul de l'angle limite, l'identification des situations où la RTI se produit, et l'application des principes à des problèmes concrets.

Exercice 1 : Calcul de l'Angle Limite

Énoncé : Un rayon lumineux se propage dans un cristal de diamant (n = 2.42) et atteint la surface de séparation avec l'air (n = 1.00). Calculer l'angle limite pour la réflexion totale interne. Solution : On utilise la formule : sin(θc) = n2 / n1. Ici, n1 = 2.42 (diamant) et n2 = 1.00 (air). Donc, sin(θc) = 1.00 / 2.42 ≈ 0.413. θc = arcsin(0.413) ≈ 24.4°. L'angle limite est donc d'environ 24.4°.

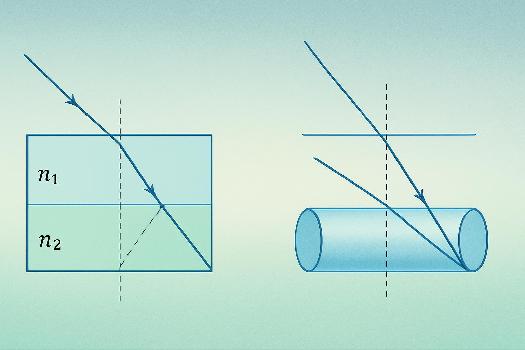
Exercice 2 : Identification de la Réflexion Totale Interne

Énoncé : Un rayon lumineux se propage de l'eau (n = 1.33) vers le verre (n = 1.50) avec un angle d'incidence de 30°. Y aura-t-il réflexion totale interne ? Justifier votre réponse. Solution : La réflexion totale interne ne peut se produire que si la lumière se propage d'un milieu d'indice de réfraction élevé vers un milieu d'indice plus faible. Dans ce cas, la lumière se propage de l'eau (n = 1.33) vers le verre (n = 1.50), donc n1 < n2. Par conséquent, il n'y aura pas de réflexion totale interne, quelle que soit la valeur de l'angle d'incidence. Il y aura réfraction.

Exercice 3 : Fibre Optique

Énoncé : Une fibre optique est constituée d'un cœur de verre (nc = 1.48) et d'une gaine de verre (ng = 1.46). Quel est l'angle maximum d'incidence à l'entrée de la fibre (par rapport à l'axe de la fibre) pour que la lumière puisse se propager à l'intérieur de la fibre par réflexion totale interne ? Solution : Pour que la lumière se propage par RTI, l'angle d'incidence au niveau de l'interface cœur-gaine doit être supérieur à l'angle limite. D'abord, calculons l'angle limite : sin(θc) = ng / nc = 1.46 / 1.48 ≈ 0.986. θc = arcsin(0.986) ≈ 80.6°. L'angle d'incidence θi au niveau de l'entrée de la fibre est lié à l'angle d'incidence θc à l'intérieur de la fibre par la loi de Snell-Descartes. L'angle maximal d'incidence à l'entrée est environ 16.9 degres. Remarque : Cet exercice nécessite des connaissances supplémentaires sur la loi de Snell-Descartes et la géométrie des fibres optiques.

Ce qu'il faut retenir

  • Pour calculer l'angle limite, utilisez la formule sin(θc) = n2 / n1.
  • La réflexion totale interne ne se produit que si n1 > n2.
  • Les fibres optiques utilisent la RTI pour guider la lumière. Le calcul de l'angle d'incidence maximal nécessite d'utiliser la loi de Snell-Descartes.

← Exercices Corrigés : Maîtriser les Prismes et la Dispersion Lumineuse Formation des images par les lentilles minces : Relation de conjugaison et Grandissement →

FAQ

  • Pourquoi utilise-t-on la réflexion totale interne dans les fibres optiques ?

    La réflexion totale interne permet de transmettre la lumière à travers la fibre optique avec très peu de perte d'intensité. C'est beaucoup plus efficace que la réflexion partielle ou la transmission à travers un matériau absorbant.
  • Comment l'angle d'incidence affecte-t-il la réflexion totale interne ?

    Si l'angle d'incidence est inférieur à l'angle limite, la lumière est réfractée. Si l'angle d'incidence est supérieur à l'angle limite, la lumière subit une réflexion totale interne. L'angle d'incidence doit être suffisamment grand pour que la condition θi > θc soit remplie.