Physique-Chimie > Optique > Optique Géométrique > Prismes (dispersion de la lumière)

Prismes et Dispersion de la Lumière : Comprendre et Maîtriser

Explorez en détail le phénomène de dispersion de la lumière à travers les prismes. Ce cours complet aborde les principes fondamentaux, les calculs d'indice de réfraction et des applications pratiques, spécialement conçu pour les élèves de lycée.

Introduction aux Prismes Optiques

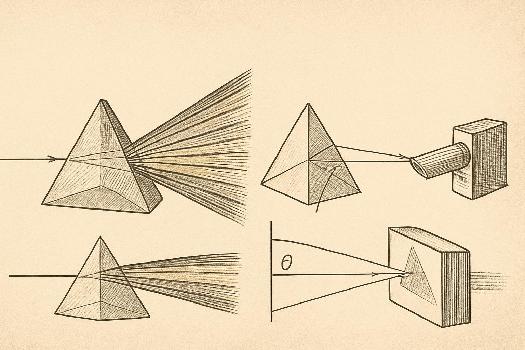
Un prisme optique est un corps transparent, généralement en verre ou en plastique, délimité par des surfaces planes. La forme la plus courante est celle d'un prisme triangulaire. Sa fonction principale est de réfracter la lumière, c'est-à-dire de dévier sa trajectoire. Plus précisément, un prisme est utilisé pour séparer la lumière blanche en ses différentes couleurs constitutives, un phénomène appelé dispersion.

Réfraction de la Lumière à l'Interface Air-Verre

Quand un rayon lumineux passe de l'air dans le verre (ou tout autre milieu transparent), il subit une réfraction. L'angle d'incidence (l'angle entre le rayon incident et la normale à la surface) et l'angle de réfraction (l'angle entre le rayon réfracté et la normale) sont liés par la loi de Snell-Descartes : n1 sin(θ1) = n2 sin(θ2) où n1 et n2 sont les indices de réfraction des milieux 1 et 2, et θ1 et θ2 sont les angles d'incidence et de réfraction, respectivement. L'indice de réfraction d'un milieu indique à quel point la lumière ralentit dans ce milieu par rapport au vide.

Dispersion de la Lumière Blanche

La lumière blanche est en réalité une combinaison de toutes les couleurs du spectre visible. L'indice de réfraction d'un matériau dépend légèrement de la longueur d'onde de la lumière. Cette dépendance est ce qui cause la dispersion. Concrètement, la lumière bleue (longueur d'onde plus courte) est plus déviée que la lumière rouge (longueur d'onde plus longue). C'est pourquoi, lorsqu'un faisceau de lumière blanche traverse un prisme, les différentes couleurs se séparent, créant un spectre visible.

Angle de Déviation Minimale

Pour un prisme donné et une longueur d'onde donnée, il existe un angle d'incidence pour lequel la déviation du rayon lumineux est minimale. Cet angle de déviation minimale (Dmin) est important car il permet de déterminer l'indice de réfraction du matériau du prisme avec une grande précision. La formule reliant l'indice de réfraction (n), l'angle au sommet du prisme (A) et l'angle de déviation minimale (Dmin) est : n = sin((A + Dmin)/2) / sin(A/2).

Calcul de l'Indice de Réfraction

Si vous connaissez l'angle au sommet (A) de votre prisme et que vous avez mesuré l'angle de déviation minimale (Dmin) pour une couleur spécifique, vous pouvez calculer l'indice de réfraction (n) du matériau pour cette couleur. C'est une application pratique de la loi de Snell-Descartes et de la compréhension de la dispersion.

Applications des Prismes

Les prismes ont de nombreuses applications pratiques, notamment :

  • Spectroscopie : Les prismes sont utilisés dans les spectromètres pour séparer la lumière en ses différentes longueurs d'onde, ce qui permet d'analyser la composition de la matière.
  • Instruments d'optique : Les prismes sont utilisés dans les jumelles, les télescopes et les appareils photo pour redresser l'image et améliorer la qualité optique.
  • Effets spéciaux : Les prismes sont utilisés pour créer des effets visuels spéciaux dans l'éclairage et la photographie.

Ce qu'il faut retenir

  • Un prisme est un objet transparent qui réfracte la lumière.
  • La dispersion est la séparation de la lumière blanche en ses couleurs constitutives à cause de la variation de l'indice de réfraction avec la longueur d'onde.
  • La loi de Snell-Descartes régit la réfraction de la lumière.
  • L'angle de déviation minimale permet de calculer l'indice de réfraction du matériau du prisme.
  • Les prismes ont de nombreuses applications en spectroscopie et dans les instruments d'optique.

← Nature Ondulatoire de la Lumière: Comprendre et Expliquer Propagation Rectiligne de la Lumière : Cours Complet →

FAQ

  • Pourquoi la lumière bleue est-elle plus déviée que la lumière rouge ?

    L'indice de réfraction d'un matériau est légèrement plus élevé pour la lumière bleue (courte longueur d'onde) que pour la lumière rouge (longue longueur d'onde). Par conséquent, la lumière bleue est plus ralentie et donc plus déviée lorsqu'elle passe dans le prisme.
  • Qu'est-ce que l'angle de déviation minimale et pourquoi est-il important ?

    L'angle de déviation minimale est l'angle de déviation le plus petit possible qu'un rayon lumineux peut subir en traversant un prisme. Il est important car il simplifie le calcul de l'indice de réfraction du matériau du prisme.
  • Peut-on utiliser un prisme pour créer un arc-en-ciel artificiel ?

    Oui, c'est exactement le principe. Un prisme sépare la lumière blanche en ses couleurs composantes, créant un spectre similaire à celui d'un arc-en-ciel. L'arc-en-ciel naturel est créé par la réfraction et la réflexion de la lumière du soleil par les gouttelettes d'eau dans l'atmosphère.