Physique-Chimie > Mécanique > Cinématique > Vecteur position, vecteur vitesse, vecteur accélération

Vecteur Position, Vitesse et Accélération : Une Introduction Complète

Comprendre les vecteurs position, vitesse et accélération est essentiel en cinématique. Cette ressource explique ces concepts avec des exemples clairs et des illustrations pour les élèves du lycée.

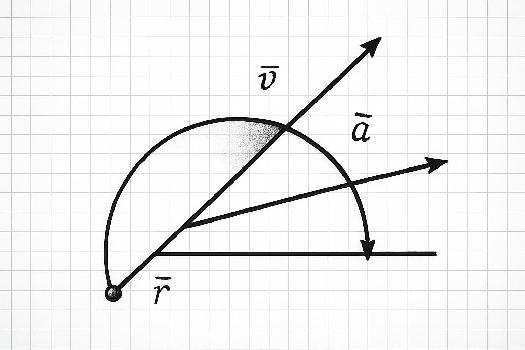
Vecteur Position

Le vecteur position, souvent noté r, décrit la position d'un objet dans l'espace à un instant donné par rapport à un point de référence appelé l'origine. Imaginez un point dans une pièce. Pour le définir, vous devez indiquer sa position par rapport à un coin de la pièce que vous prenez comme origine.

Mathématiquement, dans un repère cartésien (x, y, z), le vecteur position s'écrit : r = xi + yj + zk, où x, y et z sont les coordonnées de l'objet et i, j et k sont les vecteurs unitaires le long des axes x, y et z respectivement.

Exemple : Un oiseau se trouve à 2 mètres à l'est, 3 mètres au nord et 1 mètre au-dessus du sol. Son vecteur position par rapport à l'origine (le coin de la pièce) est donc r = 2i + 3j + 1k.

Vecteur Vitesse

Le vecteur vitesse, souvent noté v, décrit la vitesse à laquelle la position d'un objet change dans le temps, ainsi que la direction de ce mouvement. C'est donc la dérivée du vecteur position par rapport au temps.

Mathématiquement : v = dr/dt = (dx/dt)i + (dy/dt)j + (dz/dt)k. Les composantes dx/dt, dy/dt et dz/dt représentent les vitesses selon les axes x, y et z respectivement.

Exemple : Si la position de l'oiseau change au cours du temps et que sa position est donnée par r(t) = (2+t)i + (3+2t)j + (1+0.5t)k, alors sa vitesse est v = dr/dt = 1i + 2j + 0.5k m/s. Cela signifie que l'oiseau se déplace vers l'est à 1 m/s, vers le nord à 2 m/s et vers le haut à 0.5 m/s.

Vecteur Accélération

Le vecteur accélération, souvent noté a, décrit la vitesse à laquelle la vitesse d'un objet change dans le temps. C'est donc la dérivée du vecteur vitesse par rapport au temps, ou la dérivée seconde du vecteur position par rapport au temps.

Mathématiquement : a = dv/dt = d²r/dt² = (d²x/dt²)i + (d²y/dt²)j + (d²z/dt²)k. Les composantes d²x/dt², d²y/dt² et d²z/dt² représentent les accélérations selon les axes x, y et z respectivement.

Exemple : Si la vitesse de l'oiseau change au cours du temps et que sa vitesse est donnée par v(t) = (1+0.2t)i + (2-0.1t)j + 0.5k, alors son accélération est a = dv/dt = 0.2i - 0.1j + 0k m/s². Cela signifie que l'oiseau accélère vers l'est à 0.2 m/s² et décélère vers le nord à 0.1 m/s².

Relations importantes

Comprendre la relation entre la position, la vitesse et l'accélération est crucial.

Voici un résumé:

  • Vitesse et position: La vitesse est la dérivée temporelle de la position: v = dr/dt. C'est-à-dire, la vitesse indique comment la position change au fil du temps.
  • Accélération et vitesse: L'accélération est la dérivée temporelle de la vitesse: a = dv/dt. Cela signifie que l'accélération décrit comment la vitesse change au fil du temps.
  • Intégration: Inversement, la position est l'intégrale temporelle de la vitesse, et la vitesse est l'intégrale temporelle de l'accélération. Ces intégrations nécessitent des conditions initiales.

Mouvement Rectiligne Uniforme (MRU)

Dans un mouvement rectiligne uniforme (MRU), l'objet se déplace en ligne droite à une vitesse constante. Donc, l'accélération est nulle.

Les vecteurs position et vitesse sont alors :

  • r(t) = r₀ + v*t, où r₀ est la position initiale.
  • v(t) = constant, car l'accélération est nulle.

Mouvement Rectiligne Uniformément Varié (MRUV)

Dans un mouvement rectiligne uniformément varié (MRUV), l'objet se déplace en ligne droite avec une accélération constante.

Les vecteurs position et vitesse sont alors :

  • r(t) = r₀ + v₀*t + 0.5*a*t², où r₀ est la position initiale et v₀ est la vitesse initiale.
  • v(t) = v₀ + a*t.

Ce qu'il faut retenir

  • Vecteur Position (r): Décrit la position d'un objet dans l'espace par rapport à une origine.
  • Vecteur Vitesse (v): Décrit la vitesse de changement de position d'un objet et sa direction. C'est la dérivée de r par rapport au temps.
  • Vecteur Accélération (a): Décrit la vitesse de changement de la vitesse d'un objet. C'est la dérivée de v par rapport au temps (ou la dérivée seconde de r par rapport au temps).
  • MRU: Mouvement rectiligne uniforme (vitesse constante, accélération nulle).
  • MRUV: Mouvement rectiligne uniformément varié (accélération constante).

← Travail des Forces et Énergie Mécanique : Interactions et Transformations Énergie Mécanique : Comprendre et Maîtriser les Concepts Clés →

FAQ

  • Quelle est la différence entre vitesse et accélération ?

    La vitesse décrit à quelle vitesse la position change, tandis que l'accélération décrit à quelle vitesse la vitesse change. En d'autres termes, la vitesse décrit le mouvement, tandis que l'accélération décrit le changement de mouvement.
  • Comment calculer la vitesse si je connais la position en fonction du temps ?

    Vous devez dériver le vecteur position par rapport au temps. Si r(t) = x(t)i + y(t)j + z(t)k, alors v(t) = (dx/dt)i + (dy/dt)j + (dz/dt)k.
  • Comment calculer la position si je connais la vitesse en fonction du temps ?

    Vous devez intégrer le vecteur vitesse par rapport au temps. Si v(t) = vx(t)i + vy(t)j + vz(t)k, alors r(t) = (∫vx(t)dt)i + (∫vy(t)dt)j + (∫vz(t)dt)k + r₀, où r₀ est la position initiale.