Physique-Chimie > Optique > Optique Géométrique > Formation des images par les lentilles minces (relation de conjugaison, grandissement)

Formation des images par les lentilles minces : Relation de conjugaison et Grandissement

Explorez en détail la formation des images par les lentilles minces, en comprenant la relation de conjugaison et le grandissement. Ce guide complet vous fournira les bases théoriques et les outils nécessaires pour analyser et prédire la formation des images à travers les lentilles convergentes et divergentes.

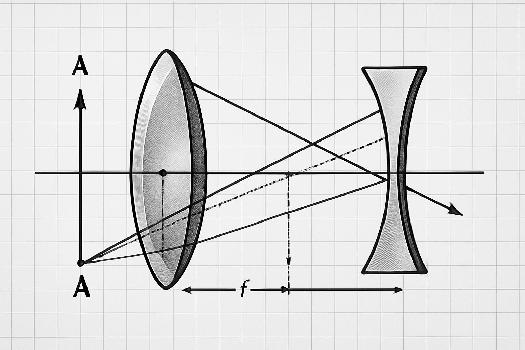
Introduction aux lentilles minces

Les lentilles minces sont des éléments optiques transparents qui réfractent la lumière, modifiant ainsi la direction des rayons lumineux. Elles sont caractérisées par deux surfaces réfringentes, généralement sphériques, et une épaisseur négligeable par rapport aux rayons de courbure de ces surfaces. On distingue principalement deux types de lentilles : les lentilles convergentes, qui font converger les rayons lumineux, et les lentilles divergentes, qui les font diverger. La compréhension des lentilles minces est cruciale en optique géométrique, car elles sont à la base de nombreux instruments optiques tels que les lunettes, les microscopes et les télescopes.

Éléments caractéristiques d'une lentille mince

Pour comprendre le fonctionnement d'une lentille mince, il est essentiel de connaître ses éléments caractéristiques :

  • Centre optique (O) : Point de la lentille où un rayon lumineux passant par ce point n'est pas dévié.
  • Axe optique : Droite passant par les centres de courbure des deux faces de la lentille.
  • Foyer principal objet (F) : Point situé sur l'axe optique tel que tout rayon incident parallèle à l'axe optique émerge en passant par le foyer image (F').
  • Foyer principal image (F') : Point situé sur l'axe optique tel que tout rayon incident passant par le foyer objet (F) émerge parallèle à l'axe optique.
  • Distance focale (f) : Distance entre le centre optique de la lentille et chacun des foyers (F et F'). La distance focale est positive pour une lentille convergente et négative pour une lentille divergente.

Construction géométrique des images

La construction géométrique d'une image formée par une lentille mince se base sur le tracé de rayons lumineux particuliers :

  • Rayon passant par le centre optique (O) : Ce rayon n'est pas dévié.
  • Rayon parallèle à l'axe optique : Ce rayon émerge de la lentille en passant par le foyer image (F') si la lentille est convergente, ou en semblant provenir du foyer objet (F) si la lentille est divergente.
  • Rayon passant par le foyer objet (F) : Ce rayon émerge de la lentille parallèle à l'axe optique si la lentille est convergente, ou en se dirigeant vers le foyer image (F') si la lentille est divergente.
L'intersection de deux de ces rayons émergents (ou de leurs prolongements) détermine la position de l'image. La nature de l'image (réelle ou virtuelle, droite ou inversée, agrandie ou réduite) dépend de la position de l'objet par rapport à la lentille.

Relation de conjugaison (Formule de Descartes)

La relation de conjugaison, également connue sous le nom de formule de Descartes, relie la position de l'objet (OA), la position de l'image (OA') et la distance focale (f) de la lentille :
1/OA' - 1/OA = 1/f'
Où:

  • OA est la distance entre l'objet et le centre optique de la lentille. Cette distance est généralement négative si l'objet est situé avant la lentille (convention de signes).
  • OA' est la distance entre l'image et le centre optique de la lentille. Cette distance est positive si l'image est réelle (située après la lentille) et négative si l'image est virtuelle (située avant la lentille).
  • f' est la distance focale de la lentille (positive pour une lentille convergente et négative pour une lentille divergente).
Cette formule est fondamentale pour calculer la position de l'image formée par une lentille mince, connaissant la position de l'objet et la distance focale de la lentille.

Exemple: Une lentille convergente a une distance focale de 10 cm. Un objet est placé à 20 cm de la lentille. Où se forme l'image ?
1/OA' - 1/(-20) = 1/10
1/OA' = 1/10 - 1/20 = 1/20
OA' = 20 cm. L'image est réelle et se forme à 20 cm de la lentille.

Grandissement

Le grandissement (γ) est le rapport entre la taille de l'image (A'B') et la taille de l'objet (AB) :
γ = A'B'/AB = OA'/OA
Où:

  • A'B' est la taille de l'image.
  • AB est la taille de l'objet.
  • OA' est la distance entre l'image et le centre optique de la lentille.
  • OA est la distance entre l'objet et le centre optique de la lentille.
Le grandissement indique si l'image est agrandie (|γ| > 1), réduite (|γ| < 1) ou de même taille (|γ| = 1) que l'objet. De plus, le signe du grandissement indique si l'image est droite (γ > 0) ou inversée (γ < 0) par rapport à l'objet.

Exemple: Dans l'exemple précédent, si l'objet mesure 5 cm, quelle est la taille de l'image ?
γ = OA'/OA = 20/(-20) = -1
A'B' = γ * AB = -1 * 5 = -5 cm. L'image est inversée et a la même taille que l'objet.

Lentilles convergentes et divergentes : Récapitulatif

Il est essentiel de distinguer clairement le comportement des lentilles convergentes et divergentes :

  • Lentilles convergentes :
    • Distance focale (f') positive.
    • Peuvent former des images réelles ou virtuelles, selon la position de l'objet.
    • Sont utilisées pour corriger l'hypermétropie.
  • Lentilles divergentes :
    • Distance focale (f') négative.
    • Forment toujours des images virtuelles, droites et réduites.
    • Sont utilisées pour corriger la myopie.

Ce qu'il faut retenir

  • Lentilles minces : Éléments optiques qui réfractent la lumière. On distingue les lentilles convergentes et divergentes.
  • Éléments caractéristiques : Centre optique (O), axe optique, foyer principal objet (F), foyer principal image (F'), distance focale (f').
  • Construction géométrique : Utiliser des rayons particuliers (passant par O, parallèle à l'axe, passant par F) pour déterminer la position et la nature de l'image.
  • Relation de conjugaison (Descartes) : 1/OA' - 1/OA = 1/f'. Permet de calculer la position de l'image.
  • Grandissement : γ = A'B'/AB = OA'/OA. Indique la taille et l'orientation de l'image par rapport à l'objet.
  • Lentilles convergentes : f' > 0, peuvent former des images réelles ou virtuelles.
  • Lentilles divergentes : f' < 0, forment toujours des images virtuelles, droites et réduites.

← Exercices Corrigés sur la Réflexion Totale Interne L'Expérience des Fentes de Young : Une Preuve de la Nature Ondulatoire de la Lumière →

FAQ

  • Comment savoir si une image est réelle ou virtuelle ?

    Une image est réelle si elle est formée par l'intersection effective des rayons lumineux après leur passage à travers la lentille. Elle peut être projetée sur un écran. Une image est virtuelle si elle est formée par le prolongement des rayons lumineux. Elle ne peut pas être projetée sur un écran et ne peut être observée qu'à travers la lentille.
  • Qu'est-ce que la convention de signes en optique ?

    La convention de signes est un ensemble de règles qui permettent de définir les signes des distances et des tailles en optique géométrique. En général, on considère que les distances mesurées dans le sens de la propagation de la lumière sont positives, et les distances mesurées dans le sens opposé sont négatives. De même, les tailles des objets et des images sont positives si elles sont orientées vers le haut, et négatives si elles sont orientées vers le bas.
  • Comment utiliser la relation de conjugaison si j'ai une lentille divergente ?

    La relation de conjugaison reste la même, mais il est crucial de se rappeler que la distance focale (f') d'une lentille divergente est négative. N'oubliez pas non plus que si l'image est virtuelle, OA' sera également négatif.