La Loi de Coulomb : Fondements et Applications

Introduction à l'Électrostatique

L'électrostatique est la branche de la physique qui étudie les charges électriques au repos. Avant d'aborder la loi de Coulomb, il est crucial de comprendre la notion de charge électrique. Il existe deux types de charges électriques : positives et négatives. Les charges de même signe se repoussent, tandis que les charges de signes opposés s'attirent. Les charges électriques sont quantifiées, c'est-à-dire qu'elles ne peuvent exister que sous forme de multiples entiers d'une charge élémentaire, notée 'e', qui est la charge d'un proton (positive) ou d'un électron (négative). La valeur de cette charge élémentaire est approximativement e = 1.602 × 10^-19 Coulombs (C).

Énoncé de la Loi de Coulomb

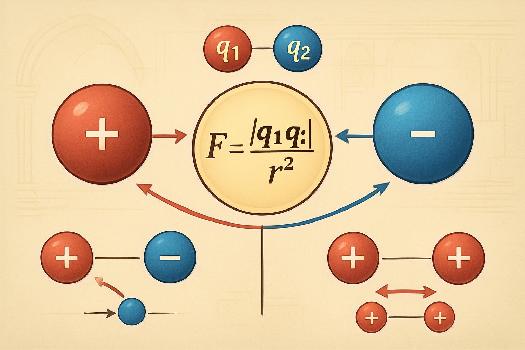
La loi de Coulomb, formulée par Charles-Augustin de Coulomb au XVIIIe siècle, quantifie la force électrostatique entre deux charges ponctuelles. Elle stipule que la force entre deux charges est directement proportionnelle au produit des valeurs absolues des charges et inversement proportionnelle au carré de la distance qui les sépare. Mathématiquement, elle s'exprime par la formule :

F = k * (|q1 * q2|) / r²

Où :

• F est la force électrostatique (en Newtons, N)
• q1 et q2 sont les valeurs des charges (en Coulombs, C)
• r est la distance entre les charges (en mètres, m)
• k est la constante de Coulomb (k ≈ 8.9875 × 10⁹ N⋅m²/C²)

Analyse Vectorielle de la Force de Coulomb

Bien que la formule scalaire donne l'amplitude de la force, il est souvent nécessaire de considérer la force comme un vecteur. Pour cela, on utilise la forme vectorielle de la loi de Coulomb :

F₁₂ = k * (q₁ * q₂ / r²) * û₁₂

Où :

• F₁₂ est la force exercée par la charge q₁ sur la charge q₂ (en vecteur).
• û₁₂ est un vecteur unitaire pointant de la charge q₁ vers la charge q₂. Sa magnitude est de 1 et sa direction est celle de la ligne reliant les deux charges.

Exemples d'Application de la Loi de Coulomb

Exemple 1 : Deux charges ponctuelles, q1 = +2 μC et q2 = -3 μC, sont séparées par une distance de 20 cm. Calculer la force électrostatique entre elles.

Solution :

1. Convertir les unités : q1 = 2 × 10^-6 C, q2 = -3 × 10^-6 C, r = 0.2 m
2. Appliquer la loi de Coulomb : F = k * (|q1 * q2|) / r² = (8.9875 × 10⁹ N⋅m²/C²) * (|(2 × 10^-6 C) * (-3 × 10^-6 C)|) / (0.2 m)²
3. Calculer : F ≈ 1.35 N
La force est attractive (car les charges sont de signes opposés).

Exemple 2 : Trois charges ponctuelles sont placées sur une ligne. q1 = +4 μC est à x = 0 m, q2 = -5 μC est à x = 0.2 m, et q3 = +6 μC est à x = 0.4 m. Calculer la force résultante sur q3.

Solution :

1. Calculer la force exercée par q1 sur q3 (F13) et la force exercée par q2 sur q3 (F23).
2. Utiliser la loi de Coulomb pour chaque paire.
3. Puisque les charges sont sur une ligne, les forces sont colinéaires. Il faut faire attention aux signes (attractives ou répulsives) pour additionner ou soustraire les magnitudes.
4. La force résultante sur q3 est la somme vectorielle de F13 et F23.

Limitations et Considérations

• Charges ponctuelles : La loi de Coulomb est rigoureusement valable pour des charges ponctuelles. Dans les situations réelles, si les objets chargés ont une certaine taille, il faut considérer la distribution de charge et intégrer les forces sur toute la surface des objets.
• Milieu : La constante de Coulomb (k) est donnée pour le vide. Si les charges sont immergées dans un autre milieu (par exemple, de l'eau), la force électrostatique sera modifiée par la constante diélectrique du milieu. La constante de Coulomb devient alors k/ε_r, où ε_r est la permittivité relative du milieu.
• Superposition : Si plus de deux charges sont présentes, la force résultante sur une charge donnée est la somme vectorielle des forces exercées par toutes les autres charges.
• Champ Électrique : La loi de Coulomb est intimement liée à la notion de champ électrique. On peut définir le champ électrique E créé par une charge q à une distance r comme la force par unité de charge qu'elle exercerait sur une charge test positive placée en ce point. E = k * (q / r²) * û. La force sur une charge q' placée dans ce champ est alors F = q'E.

Ce qu'il faut retenir

• La loi de Coulomb décrit la force électrostatique entre deux charges ponctuelles.
• F = k * (|q1 * q2|) / r², où F est la force, q1 et q2 sont les charges, r est la distance, et k est la constante de Coulomb.
• La force est attractive si les charges sont de signes opposés et répulsive si les charges sont de même signe.
• La force est une grandeur vectorielle, et la force résultante sur une charge est la somme vectorielle des forces exercées par toutes les autres charges.
• La loi de Coulomb est une loi fondamentale de l'électrostatique et est essentielle pour comprendre les interactions électriques.