Physique-Chimie > Électricité et Magnétisme > Circuits Électriques en Courant Continu > Lois de Kirchhoff (nœuds et mailles)
Applications Avancées des Lois de Kirchhoff
Exploration des applications des lois de Kirchhoff dans des circuits complexes, incluant des résistances en série et en parallèle, et des exemples de résolution de circuits avec plusieurs sources de tension.
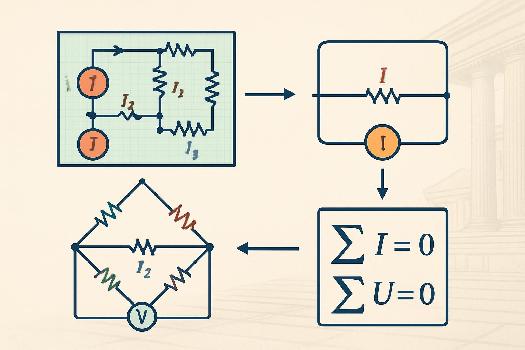
Circuits avec Résistances en Série et Parallèle
Les lois de Kirchhoff deviennent particulièrement utiles lorsqu'on analyse des circuits contenant des combinaisons de résistances en série et en parallèle. Il est crucial de comprendre comment ces configurations affectent la distribution du courant et de la tension. <ul> <li><strong>Résistances en série:</strong> Le même courant traverse toutes les résistances. La tension totale est la somme des tensions aux bornes de chaque résistance.</li> <li><strong>Résistances en parallèle:</strong> La tension est la même aux bornes de toutes les résistances. Le courant total est la somme des courants traversant chaque résistance.</li> </ul> L'application judicieuse des lois d'Ohm et des lois de Kirchhoff permet de simplifier l'analyse et de déterminer les valeurs de courant et de tension inconnues.
Circuits avec Plusieurs Sources de Tension
Lorsque des circuits contiennent plusieurs sources de tension, la superposition des effets peut compliquer l'analyse. Les lois de Kirchhoff offrent une méthode systématique pour traiter ces circuits. <ol> <li><strong>Identifier les mailles:</strong> Déterminer toutes les boucles fermées dans le circuit.</li> <li><strong>Attribuer les courants:</strong> Choisir une direction pour chaque courant dans chaque branche.</li> <li><strong>Écrire les équations de maille:</strong> Appliquer la loi des mailles à chaque boucle, en tenant compte des polarités des sources de tension et des résistances.</li> <li><strong>Résoudre le système:</strong> Résoudre le système d'équations pour trouver les courants inconnus.</li> </ol> Il est important de maintenir une convention de signe cohérente lors de l'écriture des équations de maille.
Exemple Complexe : Pont de Wheatstone
Le pont de Wheatstone est un circuit couramment utilisé pour mesurer avec précision des résistances inconnues. Il se compose de quatre résistances disposées en losange, avec une source de tension alimentant le circuit et un détecteur (galvanomètre) mesurant le courant entre les deux points médians du losange. <strong>Analyse :</strong> Pour analyser un pont de Wheatstone, il est nécessaire d'appliquer les lois de Kirchhoff aux nœuds et aux mailles du circuit. Si le pont est équilibré (aucun courant ne traverse le galvanomètre), la résistance inconnue peut être calculée en fonction des autres résistances connues. <strong>Applications :</strong> Les ponts de Wheatstone sont utilisés dans divers capteurs et instruments de mesure, tels que les thermistances (capteurs de température) et les jauges de contrainte.
Techniques de Simplification de Circuits
Dans certains cas, il est possible de simplifier les circuits complexes avant d'appliquer les lois de Kirchhoff. Voici quelques techniques : <ul> <li><strong>Combinaison de résistances en série et parallèle:</strong> Remplacer les groupes de résistances en série par leur résistance équivalente (R<sub>eq</sub> = R1 + R2 + ...). Remplacer les groupes de résistances en parallèle par leur résistance équivalente (1/R<sub>eq</sub> = 1/R1 + 1/R2 + ...).</li> <li><strong>Transformations étoile-triangle (Y-Δ):</strong> Convertir des configurations de résistances en étoile (Y) en configurations en triangle (Δ) et vice versa, ce qui peut simplifier l'analyse de certains circuits.</li> </ul>
Erreurs Courantes et Comment les Éviter
Lors de l'application des lois de Kirchhoff, certaines erreurs sont fréquemment commises : <ul> <li><strong>Mauvaise attribution des directions de courant:</strong> Choisir une direction arbitraire pour les courants est correct, mais il est crucial de maintenir cette convention tout au long de l'analyse. Si une direction est incorrecte, le courant résultant sera négatif.</li> <li><strong>Erreurs de signe dans les équations de maille:</strong> Être attentif aux polarités des sources de tension et aux directions du courant lors du parcours des mailles.</li> <li><strong>Nombre insuffisant d'équations:</strong> S'assurer d'avoir autant d'équations indépendantes que d'inconnues (courants ou tensions) pour pouvoir résoudre le système.</li> </ul>
Ce qu'il faut retenir
<ul> <li>Les lois de Kirchhoff sont essentielles pour l'analyse de circuits complexes avec résistances en série et en parallèle, et avec plusieurs sources de tension.</li> <li>La simplification des circuits peut faciliter l'application des lois de Kirchhoff.</li> <li>Le pont de Wheatstone est une application pratique des lois de Kirchhoff pour la mesure précise de résistances.</li> <li>Il est crucial d'éviter les erreurs courantes liées aux conventions de signe et au nombre d'équations.</li> </ul>
FAQ
-
Comment savoir si j'ai suffisamment d'équations pour résoudre un circuit ?
Vous devez avoir autant d'équations indépendantes que d'inconnues (courants ou tensions). Chaque application correcte de la loi des nœuds ou de la loi des mailles fournit une équation indépendante. -
Peut-on utiliser les lois de Kirchhoff pour des circuits avec des condensateurs et des inductances ?
Oui, les lois de Kirchhoff sont applicables aux circuits contenant des condensateurs et des inductances. Cependant, l'analyse devient plus complexe car les relations courant-tension pour ces composants impliquent des dérivées et des intégrales. -
Quelle est la différence entre l'analyse nodale et l'analyse des mailles ?
L'analyse nodale (basée sur la loi des nœuds) se concentre sur la détermination des tensions aux différents nœuds du circuit. L'analyse des mailles (basée sur la loi des mailles) se concentre sur la détermination des courants dans les différentes mailles du circuit. Le choix de la méthode dépend de la complexité du circuit et du nombre d'inconnues.
