Numérique et Sciences Informatiques > Représentation des Données : Types et Encodage > Types de Données de Base > Nombres entiers (représentation binaire, décimale, hexadécimale)

Représentation des nombres entiers signés: Complément à deux

Découvrez la représentation des nombres entiers signés en utilisant la méthode du complément à deux. Apprenez à représenter des nombres positifs et négatifs et à effectuer des opérations arithmétiques.

Introduction à la représentation des entiers signés

Les ordinateurs doivent être capables de manipuler des nombres entiers positifs et négatifs. La méthode la plus courante pour représenter les entiers signés est le complément à deux. Cette méthode permet de simplifier les opérations arithmétiques (addition et soustraction) et de ne nécessiter qu'un seul circuit pour les deux types de nombres.

Le bit de signe

Dans la représentation en complément à deux, le bit le plus significatif (le bit le plus à gauche) est utilisé comme bit de signe. Si ce bit est 0, le nombre est positif. Si ce bit est 1, le nombre est négatif. Par exemple, si on utilise 8 bits, le nombre 00000101 représente +5 et le nombre 1xxxxxxx représente un nombre négatif.

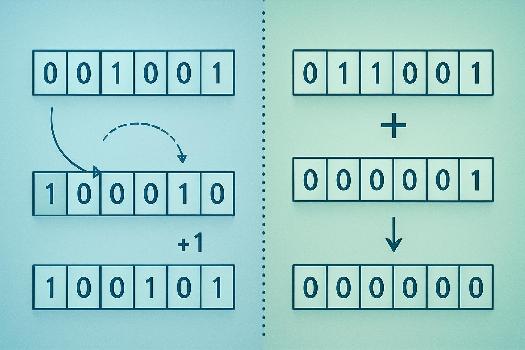
Calcul du complément à deux d'un nombre

Le complément à deux d'un nombre est obtenu en deux étapes:

  1. Inverser tous les bits du nombre (remplacer les 0 par des 1 et les 1 par des 0). C'est le complément à un.
  2. Ajouter 1 au résultat.
Par exemple, calculons le complément à deux de 5 (00000101 sur 8 bits):
  1. Inversion des bits: 11111010
  2. Ajout de 1: 11111011
Donc, -5 est représenté par 11111011 en complément à deux.

Représentation des nombres négatifs

Un nombre négatif est représenté par le complément à deux de sa valeur absolue. Reprenons l'exemple de -5: Nous avons vu que le complément à deux de 5 est 11111011. Donc -5 est représenté par 11111011. Pour vérifier, calculons le complément à deux de 11111011:

  • Inversion des bits: 00000100
  • Ajout de 1: 00000101 (qui est bien 5)

Plage de valeurs représentables

Avec une représentation sur n bits en complément à deux, on peut représenter les nombres entiers allant de -2n-1 à 2n-1 - 1. Par exemple, avec 8 bits, on peut représenter les nombres allant de -128 à 127. Il y a un nombre négatif de plus que de nombres positifs car le zéro est considéré positif.

Addition en complément à deux

L'addition en complément à deux se fait comme une addition binaire classique. Si un dépassement (carry) se produit au niveau du bit de signe, il est ignoré. Par exemple, calculons 5 + (-3) avec une représentation sur 8 bits:

  • 5 = 00000101
  • -3 = 11111101 (complément à deux de 3)
00000101 + 11111101 = 00000010 (en ignorant le dépassement). 00000010 représente 2, ce qui est bien le résultat attendu.

Soustraction en complément à deux

La soustraction peut être réalisée en additionnant le complément à deux du nombre à soustraire. Par exemple, calculons 5 - 3: 5 - 3 = 5 + (-3). On a déjà calculé que -3 est représenté par 11111101. Donc, 5 - 3 = 00000101 + 11111101 = 00000010 (en ignorant le dépassement), ce qui représente 2.

Avantages du complément à deux

  • Unicité du zéro: Il n'y a qu'une seule représentation pour zéro (00000000).
  • Simplification des opérations arithmétiques: Les additions et soustractions peuvent être effectuées avec les mêmes circuits, quel que soit le signe des nombres.
  • Facilité d'implémentation matérielle: La méthode est simple à implémenter avec des circuits logiques.

Ce qu'il faut retenir

  • Bit de signe: Le bit le plus significatif indique le signe du nombre (0 pour positif, 1 pour négatif).
  • Complément à deux: Technique de représentation des entiers signés qui permet de simplifier les opérations arithmétiques.
  • Calcul du complément à deux: Inversion des bits (complément à un) suivie d'une addition de 1.
  • Plage de valeurs: Avec n bits, on peut représenter les nombres de -2n-1 à 2n-1 - 1.
  • Addition et soustraction: Effectuées comme des opérations binaires classiques en utilisant le complément à deux.
  • Avantages: Unicité du zéro, simplification des opérations, facilité d'implémentation matérielle.

← Représentation des caractères : ASCII et UTF-8 Sons Numériques : Échantillonnage et Quantification →

FAQ

  • Pourquoi utilise-t-on le complément à deux pour représenter les nombres négatifs ?

    Le complément à deux simplifie l'implémentation des opérations arithmétiques (addition et soustraction) dans les ordinateurs. Il permet d'utiliser les mêmes circuits pour les nombres positifs et négatifs.
  • Que se passe-t-il si on dépasse la plage de valeurs représentables ?

    Un dépassement (overflow) se produit. Le résultat de l'opération est incorrect car il ne peut pas être représenté avec le nombre de bits disponibles. Par exemple, si on additionne deux grands nombres positifs et que le résultat est négatif, c'est un signe de dépassement.
  • Comment déterminer si un nombre en complément à deux est positif ou négatif ?

    Il suffit de regarder le bit le plus significatif (le bit le plus à gauche). Si c'est 0, le nombre est positif. Si c'est 1, le nombre est négatif.