Numérique et Sciences Informatiques > Numération et Bases > Systèmes de Numération > Base décimale

La Base Décimale : Notre Système de Numération Quotidien

Découvrez en détail le système de numération décimal (base 10), son fonctionnement, son histoire et son importance dans nos vies de tous les jours. Comprenez comment représenter les nombres et effectuer des opérations dans ce système fondamental.

Introduction à la Base Décimale

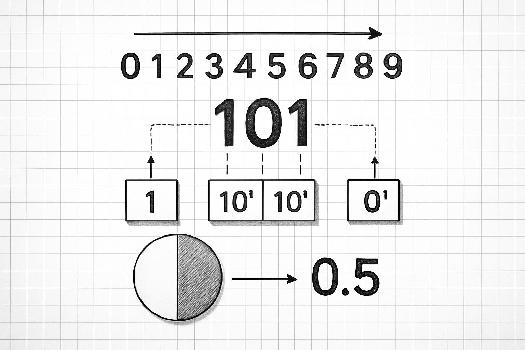
La base décimale, ou base 10, est le système de numération que nous utilisons quotidiennement. Elle est basée sur dix symboles, appelés chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. Chaque position dans un nombre décimal représente une puissance de 10. Par exemple, dans le nombre 345, le 5 représente 5 unités (100), le 4 représente 4 dizaines (101), et le 3 représente 3 centaines (102).

Valeur Positionnelle

La valeur positionnelle est le concept clé de la base décimale. Chaque chiffre a une valeur qui dépend de sa position dans le nombre.

Prenons l'exemple du nombre 1234. Sa décomposition est la suivante:

  • 1 représente 1 x 103 = 1000 (mille)
  • 2 représente 2 x 102 = 200 (deux cents)
  • 3 représente 3 x 101 = 30 (trente)
  • 4 représente 4 x 100 = 4 (quatre)

Donc, 1234 = 1000 + 200 + 30 + 4.

Représentation des Nombres Décimaux

Un nombre décimal peut être entier ou fractionnaire. Les nombres entiers sont formés uniquement de chiffres avant la virgule (ou point en notation anglo-saxonne). Les nombres fractionnaires ont une partie entière et une partie décimale séparées par une virgule.

Exemples:

  • 25 : nombre entier
  • 3.14 : nombre décimal (pi)
  • 0.75 : nombre décimal fractionnaire
La partie après la virgule représente des puissances négatives de 10. Par exemple, dans 3.14, le 1 représente 1 dixième (10-1) et le 4 représente 4 centièmes (10-2).

Opérations Arithmétiques en Base Décimale

Les opérations arithmétiques (addition, soustraction, multiplication, division) sont réalisées en base décimale de manière intuitive, grâce à notre habitude de les utiliser depuis l'enfance.

Addition: On additionne les chiffres colonne par colonne, en partant de la droite, et on retient les retenues si la somme dépasse 9.

Soustraction: Similaire à l'addition, mais on emprunte aux colonnes de gauche si nécessaire.

Multiplication: On multiplie chaque chiffre d'un nombre par chaque chiffre de l'autre nombre, puis on additionne les résultats en tenant compte des décalages.

Division: La division longue est utilisée pour diviser des nombres plus grands.

Origines et Histoire de la Base Décimale

L'origine de la base décimale est largement attribuée au fait que les humains ont dix doigts. Les premiers systèmes de numération étaient souvent basés sur le comptage avec les doigts.

Le système de numération indo-arabe, qui est le système décimal que nous utilisons aujourd'hui, s'est développé en Inde et a été diffusé dans le monde arabe, puis en Europe. L'introduction du zéro a été une avancée majeure, permettant de représenter l'absence de quantité et simplifiant les calculs.

Ce qu'il faut retenir

  • La base décimale (base 10) utilise dix chiffres (0-9).
  • La valeur de chaque chiffre dépend de sa position (valeur positionnelle).
  • Chaque position représente une puissance de 10.
  • Les nombres décimaux peuvent être entiers ou fractionnaires.
  • Le système indo-arabe, avec l'introduction du zéro, est à la base de notre système décimal actuel.

← Exercices pratiques et exemples sur la Base Hexadécimale La Base Hexadécimale : Un guide complet →

FAQ

  • Pourquoi utilise-t-on la base décimale plutôt qu'une autre base ?

    La base décimale est probablement issue du fait que nous avons dix doigts. Bien que d'autres bases soient possibles et utilisées dans certains contextes (par exemple, la base binaire en informatique), la base décimale est profondément ancrée dans notre culture et notre éducation.
  • Comment convertir un nombre d'une autre base en base décimale ?

    Pour convertir un nombre d'une autre base en base décimale, il faut multiplier chaque chiffre par la puissance de la base correspondante à sa position et additionner les résultats. Par exemple, le nombre 1101 en base 2 (binaire) est égal à (1 x 23) + (1 x 22) + (0 x 21) + (1 x 20) = 8 + 4 + 0 + 1 = 13 en base décimale.