Numérique et Sciences Informatiques > Algorithmique : Tris et Recherche > Algorithmes de Tri Efficaces > Tri fusion (Mergesort)
Tri Fusion (Mergesort) : Un Guide Complet
Comprendre le tri fusion (Mergesort) : algorithme de tri efficace, explication pas à pas, exemples concrets et complexité. Parfait pour les élèves de lycée en NSI.
Introduction au Tri Fusion
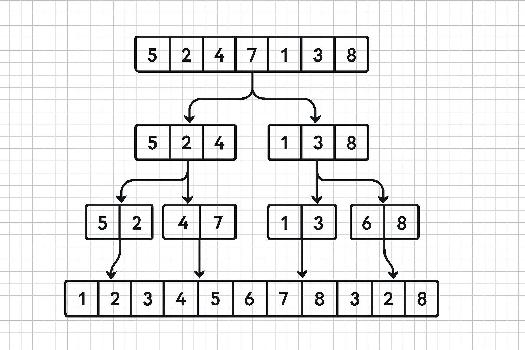
Le tri fusion, ou Mergesort, est un algorithme de tri basé sur le paradigme diviser pour régner. Il divise récursivement une liste en sous-listes plus petites jusqu'à ce que chaque sous-liste ne contienne qu'un seul élément. Ensuite, il fusionne ces sous-listes de manière répétée pour produire de nouvelles sous-listes triées, jusqu'à obtenir une seule liste triée. C'est un algorithme de tri stable et efficace, particulièrement performant pour de grands ensembles de données.
Contrairement à certains algorithmes de tri qui peuvent être plus intuitifs à première vue (comme le tri par insertion ou le tri à bulles), le tri fusion excelle en performance grâce à son approche systématique et sa complexité temporelle avantageuse.
Principe de l'Algorithme : Diviser pour Régner
Le principe fondamental du tri fusion est de décomposer le problème initial (trier une liste) en sous-problèmes plus simples, puis de combiner les solutions de ces sous-problèmes pour obtenir la solution globale.
Voici les étapes clés :
- Diviser : La liste est divisée en deux moitiés (approximativement égales).
- Régner : Chaque moitié est triée récursivement en appliquant le tri fusion. Si une moitié contient un seul élément, elle est considérée comme déjà triée (cas de base de la récursion).
- Combiner (Fusionner) : Les deux moitiés triées sont fusionnées pour former une seule liste triée. Cette étape est cruciale et réalisée de manière efficace.
L'Étape de Fusion : Le Cœur de l'Algorithme
L'étape de fusion est l'opération qui combine deux listes triées en une seule liste triée. Voici comment elle fonctionne en détail :
1. Initialisation : On utilise deux pointeurs (indices), un pour chaque liste triée. Ils pointent initialement sur le premier élément de chaque liste.
2. Comparaison et Ajout : On compare les éléments pointés par les deux pointeurs. Le plus petit des deux éléments est ajouté à la liste fusionnée. Le pointeur de la liste contenant l'élément ajouté est ensuite incrémenté pour pointer vers l'élément suivant.
3. Répétition : L'étape 2 est répétée jusqu'à ce que l'un des pointeurs atteigne la fin de sa liste.
4. Ajout des Éléments Restants : Une fois qu'une des listes est entièrement parcourue, tous les éléments restants de l'autre liste sont ajoutés à la fin de la liste fusionnée (ils sont déjà triés).
Exemple :
Soient deux listes triées : [1, 3, 5] et [2, 4, 6].
| Étape | Liste 1 | Liste 2 | Liste Fusionnée |
|---|---|---|---|
| Départ | [1, 3, 5] (pointeur sur 1) | [2, 4, 6] (pointeur sur 2) | [] |
| 1 | [1, 3, 5] (pointeur sur 3) | [2, 4, 6] (pointeur sur 2) | [1] |
| 2 | [1, 3, 5] (pointeur sur 3) | [2, 4, 6] (pointeur sur 4) | [1, 2] |
| 3 | [1, 3, 5] (pointeur sur 3) | [2, 4, 6] (pointeur sur 4) | [1, 2, 3] |
| 4 | [1, 3, 5] (pointeur sur 5) | [2, 4, 6] (pointeur sur 4) | [1, 2, 3, 4] |
| 5 | [1, 3, 5] (pointeur sur 5) | [2, 4, 6] (pointeur sur 6) | [1, 2, 3, 4, 5] |
| Fin | [1, 3, 5] (fin) | [2, 4, 6] (pointeur sur 6) | [1, 2, 3, 4, 5, 6] |
Implémentation en Python
Voici une implémentation simple du tri fusion en Python :
def tri_fusion(liste):
if len(liste) <= 1:
return liste
milieu = len(liste) // 2
gauche = liste[:milieu]
droite = liste[milieu:]
gauche = tri_fusion(gauche)
droite = tri_fusion(droite)
return fusion(gauche, droite)
def fusion(gauche, droite):
fusionne = []
i = j = 0
while i < len(gauche) and j < len(droite):
if gauche[i] < droite[j]:
fusionne.append(gauche[i])
i += 1
else:
fusionne.append(droite[j])
j += 1
fusionne += gauche[i:]
fusionne += droite[j:]
return fusionne
# Exemple d'utilisation
liste_non_triee = [12, 11, 13, 5, 6, 7]
liste_triee = tri_fusion(liste_non_triee)
print(liste_triee) # Output: [5, 6, 7, 11, 12, 13]Explication du code :
- La fonction
tri_fusiondivise la liste en deux, appelle récursivementtri_fusionsur chaque moitié, puis fusionne les résultats avec la fonctionfusion. - La fonction
fusionprend deux listes triées en entrée et les fusionne en une seule liste triée, comme expliqué précédemment.
Complexité du Tri Fusion
Le tri fusion a une complexité temporelle de O(n log n) dans tous les cas (meilleur, moyen et pire). Cela signifie que le temps d'exécution de l'algorithme croît de manière proportionnelle à n log n, où n est le nombre d'éléments dans la liste à trier. Cette complexité en fait un algorithme de tri très performant, surtout pour les grandes listes.
La complexité spatiale du tri fusion est de O(n), car il nécessite un espace supplémentaire pour stocker les sous-listes lors de la fusion. Bien que cet espace supplémentaire puisse être un inconvénient dans certains cas, la performance globale de l'algorithme justifie souvent son utilisation.
Avantages et Inconvénients
Avantages :
- Efficacité : Complexité temporelle de O(n log n) dans tous les cas.
- Stabilité : Préserve l'ordre relatif des éléments égaux.
- Bien adapté au tri de grandes quantités de données.
- Performances prédictibles: Pas de cas pathologique comme le tri rapide.
Inconvénients :
- Complexité spatiale : Nécessite un espace mémoire supplémentaire de O(n).
- Récursif : Peut entraîner une surcharge liée aux appels de fonction récursifs, bien que cela puisse être optimisé.
- Moins performant pour les très petites listes: Pour de petites listes, des algorithmes plus simples (comme le tri par insertion) peuvent être plus rapides en pratique.
Ce qu'il faut retenir
- Le tri fusion est un algorithme de tri basé sur le principe 'diviser pour régner'.
- Il divise la liste en moitiés récursivement, trie chaque moitié, puis fusionne les moitiés triées.
- L'étape de fusion est cruciale et combine efficacement deux listes triées en une seule.
- La complexité temporelle est de O(n log n), ce qui le rend efficace pour les grandes listes.
- La complexité spatiale est de O(n), ce qui signifie qu'il nécessite de l'espace mémoire supplémentaire.
- Il est stable, préservant l'ordre des éléments égaux.
- Bien qu'efficace, il peut être moins performant que des algorithmes plus simples pour de très petites listes.
FAQ
-
Pourquoi le tri fusion est-il plus efficace que le tri à bulles pour les grandes listes ?
Le tri à bulles a une complexité temporelle de O(n^2), ce qui signifie que le temps d'exécution augmente de manière quadratique avec la taille de la liste. Pour les grandes listes, cela devient prohibitif. Le tri fusion, avec sa complexité de O(n log n), croît beaucoup plus lentement, ce qui le rend beaucoup plus rapide pour les grandes quantités de données. -
Qu'est-ce que signifie la stabilité d'un algorithme de tri ?
Un algorithme de tri est dit stable s'il préserve l'ordre relatif des éléments égaux. Par exemple, si une liste contient deux éléments avec la même valeur, leur ordre d'apparition dans la liste triée sera le même que dans la liste d'origine. Le tri fusion est un algorithme stable.
