Numérique et Sciences Informatiques > Logique Booléenne et Circuits Logiques (Bases) > Algèbre de Boole > Lois de De Morgan (notions)
Les Lois de De Morgan : Comprendre et Appliquer
Découvrez les lois de De Morgan, des outils essentiels de l'algèbre de Boole, expliquées simplement avec des exemples concrets. Apprenez à simplifier et transformer les expressions logiques. Ce cours détaillé est spécialement conçu pour les élèves de lycée.
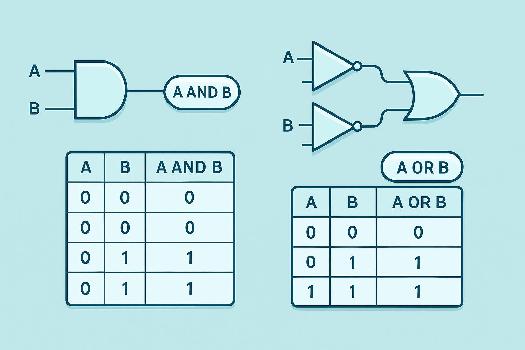
Introduction aux Lois de De Morgan
Les lois de De Morgan sont deux règles fondamentales en algèbre de Boole qui permettent de simplifier et de transformer des expressions logiques. Elles sont particulièrement utiles lorsqu'on travaille avec des opérations de négation (NON), de conjonction (ET) et de disjonction (OU). Elles portent le nom du mathématicien Augustus De Morgan.
Première Loi de De Morgan : Négation d'une Conjonction
La première loi de De Morgan stipule que la négation d'une conjonction (ET) est équivalente à la disjonction (OU) des négations de chaque élément. Formule : NON (A ET B) = (NON A) OU (NON B) Explication : Si l'expression 'A ET B' est fausse, cela signifie que soit A est faux, soit B est faux, soit les deux sont faux. Donc, 'NON A OU NON B' doit être vrai. Exemple : Supposons que A représente 'Il pleut' et B représente 'Il y a du vent'. * 'A ET B' signifie 'Il pleut ET il y a du vent'. * 'NON (A ET B)' signifie 'Il est faux qu'il pleut et qu'il y a du vent' (c'est-à-dire, il ne pleut pas ET il n'y a pas de vent, ou l'un des deux). * 'NON A' signifie 'Il ne pleut pas'. * 'NON B' signifie 'Il n'y a pas de vent'. * '(NON A) OU (NON B)' signifie 'Il ne pleut pas OU il n'y a pas de vent'. Donc, 'Il est faux qu'il pleut et qu'il y a du vent' est équivalent à 'Il ne pleut pas OU il n'y a pas de vent'.
Deuxième Loi de De Morgan : Négation d'une Disjonction
La deuxième loi de De Morgan stipule que la négation d'une disjonction (OU) est équivalente à la conjonction (ET) des négations de chaque élément. Formule : NON (A OU B) = (NON A) ET (NON B) Explication : Si l'expression 'A OU B' est fausse, cela signifie que ni A ni B ne sont vrais. Donc, 'NON A ET NON B' doit être vrai. Exemple : Reprenons les exemples précédents avec A et B. * 'A OU B' signifie 'Il pleut OU il y a du vent'. * 'NON (A OU B)' signifie 'Il est faux qu'il pleut ou qu'il y a du vent' (c'est-à-dire, ni l'un ni l'autre). * 'NON A' signifie 'Il ne pleut pas'. * 'NON B' signifie 'Il n'y a pas de vent'. * '(NON A) ET (NON B)' signifie 'Il ne pleut pas ET il n'y a pas de vent'. Donc, 'Il est faux qu'il pleut ou qu'il y a du vent' est équivalent à 'Il ne pleut pas ET il n'y a pas de vent'.
Application Pratique avec les Tables de Vérité
Les tables de vérité permettent de vérifier facilement les lois de De Morgan. On peut construire une table de vérité pour chaque côté de l'équation et vérifier qu'ils donnent les mêmes résultats pour toutes les combinaisons possibles de A et B. Table de vérité pour NON (A ET B) = (NON A) OU (NON B)
| A | B | A ET B | NON (A ET B) | NON A | NON B | (NON A) OU (NON B) |
|---|---|---|---|---|---|---|
| Vrai | Vrai | Vrai | Faux | Faux | Faux | Faux |
| Vrai | Faux | Faux | Vrai | Faux | Vrai | Vrai |
| Faux | Vrai | Faux | Vrai | Vrai | Faux | Vrai |
| Faux | Faux | Faux | Vrai | Vrai | Vrai | Vrai |
| A | B | A OU B | NON (A OU B) | NON A | NON B | (NON A) ET (NON B) |
|---|---|---|---|---|---|---|
| Vrai | Vrai | Vrai | Faux | Faux | Faux | Faux |
| Vrai | Faux | Vrai | Faux | Faux | Vrai | Faux |
| Faux | Vrai | Vrai | Faux | Vrai | Faux | Faux |
| Faux | Faux | Faux | Vrai | Vrai | Vrai | Vrai |
Exemples d'Application dans les Circuits Logiques
Les lois de De Morgan sont utilisées pour simplifier les circuits logiques, en particulier lorsqu'on manipule des portes NON-ET (NAND) et NON-OU (NOR). Une porte NAND est équivalente à une porte OU avec des entrées inversées, et une porte NOR est équivalente à une porte ET avec des entrées inversées. Cela permet de réduire le nombre de portes nécessaires et d'optimiser la conception des circuits. Exemple : Considérons un circuit qui doit réaliser la fonction NON (A ET B). Au lieu d'utiliser une porte ET suivie d'une porte NON, on peut directement utiliser une porte NAND. De même, pour réaliser la fonction NON (A OU B), on peut utiliser une porte NOR. En utilisant les lois de De Morgan, on peut transformer une expression logique complexe en une forme plus simple, ce qui facilite la conception et l'implémentation des circuits.
Ce qu'il faut retenir
- Les lois de De Morgan sont deux règles fondamentales de l'algèbre de Boole :
- Première loi : NON (A ET B) = (NON A) OU (NON B)
- Deuxième loi : NON (A OU B) = (NON A) ET (NON B)
- Elles permettent de simplifier et transformer des expressions logiques.
- Les tables de vérité permettent de vérifier ces lois.
- Elles sont utilisées pour simplifier la conception des circuits logiques, en particulier avec les portes NAND et NOR.
FAQ
-
Pourquoi les lois de De Morgan sont-elles importantes ?
Elles simplifient les expressions logiques, facilitent la conception des circuits et optimisent les ressources en réduisant le nombre de portes logiques nécessaires. -
Comment puis-je me souvenir facilement des lois de De Morgan ?
Pensez que la négation 'casse' l'opération logique et inverse les variables : une négation d'un ET devient un OU avec des négations des variables, et une négation d'un OU devient un ET avec des négations des variables.
