Numérique et Sciences Informatiques > Numération et Bases > Conversions de Bases > Décimal vers hexadécimal et inversement
Conversion Décimal-Hexadécimal et Réciproquement
Explorez en détail la conversion entre les systèmes décimal et hexadécimal, avec des exemples clairs et des méthodes pas à pas pour les lycéens.
Introduction aux Systèmes Numériques
Commençons par définir ce que sont les systèmes numériques. Un système numérique est un ensemble de symboles et de règles utilisés pour représenter des nombres. Le système décimal (base 10) est celui que nous utilisons quotidiennement, avec les chiffres 0 à 9. Le système hexadécimal (base 16) utilise les chiffres 0 à 9 et les lettres A à F, où A représente 10, B représente 11, et ainsi de suite jusqu'à F qui représente 15. La compréhension de ces systèmes est cruciale en informatique, notamment pour la représentation des couleurs, des adresses mémoire, et des données en général.
Conversion Décimal vers Hexadécimal
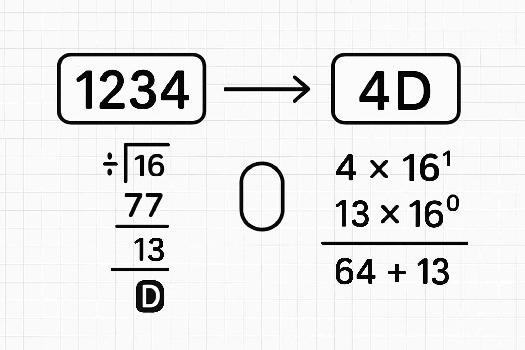
La conversion d'un nombre décimal en hexadécimal se fait en divisant successivement le nombre décimal par 16 et en conservant les restes de ces divisions. Les restes, lus de bas en haut (du dernier reste au premier), représentent le nombre hexadécimal. Voici les étapes détaillées:
- Diviser le nombre décimal par 16. Noter le quotient et le reste.
- Si le quotient est non nul, diviser le quotient par 16. Noter le nouveau quotient et le reste.
- Répéter l'étape 2 jusqu'à ce que le quotient soit nul.
- Convertir les restes supérieurs à 9 en leurs équivalents hexadécimaux (10=A, 11=B, 12=C, 13=D, 14=E, 15=F).
- Écrire les restes de bas en haut pour obtenir le nombre hexadécimal.
| Division | Quotient | Reste |
|---|---|---|
| 450 / 16 | 28 | 2 |
| 28 / 16 | 1 | 12 (C) |
| 1 / 16 | 0 | 1 |
Conversion Hexadécimal vers Décimal
La conversion d'un nombre hexadécimal en décimal se fait en multipliant chaque chiffre hexadécimal par 16 élevé à la puissance de sa position (en commençant par la position 0 à partir de la droite) et en additionnant les résultats. Voici les étapes détaillées:
- Identifier chaque chiffre hexadécimal et sa position (de droite à gauche, en commençant par 0).
- Convertir chaque chiffre hexadécimal en sa valeur décimale (A=10, B=11, C=12, D=13, E=14, F=15).
- Multiplier chaque valeur décimale par 16 élevé à la puissance de sa position.
- Additionner tous les résultats pour obtenir le nombre décimal.
- F (position 0) = 15 * 160 = 15 * 1 = 15
- A (position 1) = 10 * 161 = 10 * 16 = 160
- 2 (position 2) = 2 * 162 = 2 * 256 = 512
Applications Pratiques
La conversion entre décimal et hexadécimal est essentielle dans plusieurs domaines de l'informatique:
- Couleurs en HTML/CSS: Les couleurs sont souvent représentées en hexadécimal (par exemple, #FF0000 pour le rouge).
- Adresses mémoire: Les adresses mémoire sont souvent affichées en hexadécimal.
- Représentation des données: Les données binaires sont souvent regroupées en octets, et chaque octet est facilement représenté par deux chiffres hexadécimaux.
- Débogage: L'affichage des valeurs des variables en hexadécimal peut aider à identifier des erreurs dans le code.
Ce qu'il faut retenir
- Le système décimal est en base 10 (0-9), tandis que le système hexadécimal est en base 16 (0-9, A-F).
- Pour convertir un nombre décimal en hexadécimal, divisez successivement par 16 et conservez les restes.
- Pour convertir un nombre hexadécimal en décimal, multipliez chaque chiffre par 16 élevé à la puissance de sa position et additionnez les résultats.
- La conversion entre ces bases est cruciale pour comprendre la représentation des données en informatique (couleurs, adresses mémoire, etc.).
FAQ
-
Pourquoi utilise-t-on le système hexadécimal en informatique ?
Le système hexadécimal est utilisé car il permet de représenter facilement et de manière concise les données binaires. Chaque chiffre hexadécimal correspond à 4 bits (un demi-octet), ce qui facilite la manipulation et la lecture des données binaires. -
Comment puis-je vérifier si ma conversion est correcte ?
Vous pouvez utiliser une calculatrice en ligne ou un convertisseur de base pour vérifier vos résultats. Il existe de nombreux outils disponibles gratuitement sur internet. -
Que se passe-t-il si j'ai un nombre décimal fractionnaire à convertir en hexadécimal ?
La conversion des nombres décimaux fractionnaires en hexadécimal est plus complexe et implique des multiplications successives par 16. Pour les besoins du lycée, on se concentre généralement sur les nombres entiers.
