Opérations de Base en Binaire

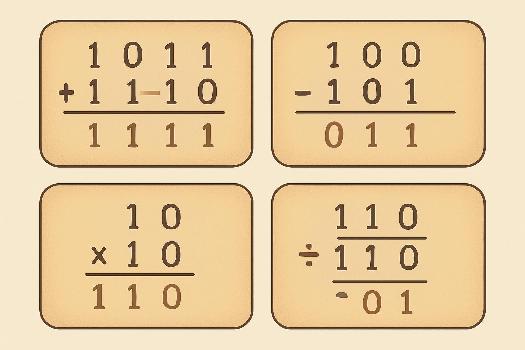
Addition Binaire

L'addition binaire suit des règles similaires à l'addition décimale, mais avec seulement deux chiffres (0 et 1). Voici les règles de base :

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 10 (0 avec une retenue de 1)

Pour additionner des nombres binaires plus longs, on procède de la même manière qu'en décimal, en tenant compte des retenues.Exemple : Additionnons les nombres binaires 1011 et 0110 :

	1	0	1	1
+	0	1	1	0
=	1	0	0	0	1

On commence par la colonne la plus à droite : 1 + 0 = 1. Puis, 1 + 1 = 10 (0 avec une retenue de 1). Ensuite, 1 (retenue) + 0 + 1 = 10 (0 avec une retenue de 1). Enfin, 1 (retenue) + 1 + 0 = 10 (0 avec une retenue de 1). La somme est donc 10001.

Soustraction Binaire

La soustraction binaire nécessite également quelques règles spécifiques :

• 0 - 0 = 0
• 1 - 0 = 1
• 1 - 1 = 0
• 0 - 1 = 1 (avec un emprunt de 1 de la colonne suivante)

Lorsqu'on doit soustraire 1 de 0, on emprunte 1 à la colonne suivante, transformant le 0 en 10 (2 en décimal), et donc 10 - 1 = 1.Exemple : Soustrayons 0110 de 1011 :

	1	0	1	1
-	0	1	1	0
=	0	1	0	1

On commence par la colonne la plus à droite : 1 - 0 = 1. Ensuite, 1 - 1 = 0. Puis, 0 - 1 nécessite un emprunt, transformant le 0 en 10 (2 en décimal), donc 10 - 1 = 1. Enfin, comme on a emprunté, le 1 de la colonne la plus à gauche devient 0, et 0 - 0 = 0. Le résultat est donc 0101.

Multiplication Binaire

La multiplication binaire est plus simple que la multiplication décimale car elle implique uniquement des multiplications par 0 ou par 1. On effectue des multiplications partielles et on les additionne ensuite.Exemple : Multiplions 101 par 11 :

		1	0	1
x			1	1
		1	0	1
+	1	0	1
=	1	1	1	1

• Première ligne : 101 x 1 = 101
• Deuxième ligne : 101 x 1 = 101 (décalé d'une position vers la gauche)
• On additionne les lignes : 101 + 1010 = 1111

Le résultat est donc 1111.

Division Binaire

La division binaire est similaire à la division décimale. On effectue des soustractions successives pour trouver le quotient et le reste.Exemple : Divisons 1101 par 10 :

• On commence par regarder si 10 rentre dans 11 (les deux premiers chiffres de 1101). Oui, il rentre une fois. On soustrait 10 de 11, ce qui donne 1.
• On abaisse le chiffre suivant (0), ce qui donne 10. 10 rentre une fois dans 10. On soustrait 10 de 10, ce qui donne 0.
• On abaisse le dernier chiffre (1), ce qui donne 1. 10 ne rentre pas dans 1. Le quotient est donc 11 et le reste est 1.

Ce qu'il faut retenir

• L'addition binaire suit des règles simples basées sur l'addition de 0 et de 1.
• La soustraction binaire nécessite parfois des emprunts.
• La multiplication binaire est simplifiée par le fait qu'on ne multiplie que par 0 ou par 1.
• La division binaire est similaire à la division décimale, avec des soustractions successives.