Numérique et Sciences Informatiques > Logique Booléenne et Circuits Logiques (Bases) > Portes Logiques > Fonctionnement
Fonctionnement des Portes Logiques : Principes et Applications
Explorez le fonctionnement interne des portes logiques fondamentales (ET, OU, NON) et leur rôle essentiel dans la construction de circuits numériques. Comprenez comment ces briques de base traitent les signaux binaires et réalisent des opérations logiques.
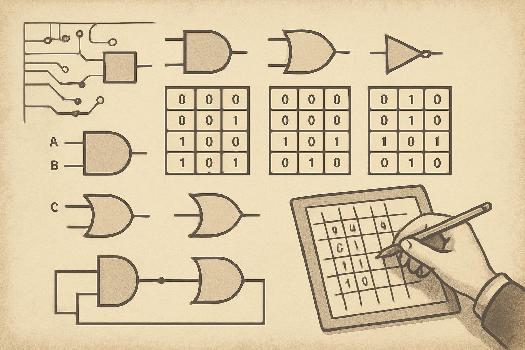
Introduction aux Portes Logiques
Les portes logiques sont les éléments constitutifs de base de tout circuit numérique. Elles reçoivent une ou plusieurs entrées et produisent une seule sortie. Chaque entrée et sortie représente une valeur booléenne, soit 0 (faux) soit 1 (vrai). Le comportement d'une porte logique est défini par sa table de vérité, qui liste toutes les combinaisons possibles d'entrées et la sortie correspondante.
La Porte ET (AND)
La porte ET a deux entrées (A et B) et une sortie (S). La sortie S est vraie (1) uniquement si les deux entrées A ET B sont vraies (1). Sinon, la sortie est fausse (0). Voici sa table de vérité :
| A | B | S (A ET B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Imaginez un interrupteur pour chaque entrée. La lampe (sortie) ne s'allume que si les DEUX interrupteurs sont fermés (position 1).
La Porte OU (OR)
La porte OU a deux entrées (A et B) et une sortie (S). La sortie S est vraie (1) si au moins l'une des entrées A OU B est vraie (1). La sortie est fausse (0) seulement si les deux entrées sont fausses (0). Voici sa table de vérité :
| A | B | S (A OU B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Imaginez toujours un interrupteur pour chaque entrée. La lampe (sortie) s'allume si AU MOINS UN des interrupteurs est fermé (position 1).
La Porte NON (NOT)
La porte NON a une seule entrée (A) et une sortie (S). La sortie S est l'inverse de l'entrée A. Si l'entrée A est vraie (1), la sortie S est fausse (0), et vice versa. On l'appelle aussi un inverseur. Voici sa table de vérité :
| A | S (NON A) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Imaginez un interrupteur qui inverse l'état. Si l'interrupteur est ouvert (position 0), la lampe (sortie) s'allume (position 1), et inversement.
Autres Portes Logiques (NAND, NOR, XOR, XNOR)
Il existe d'autres portes logiques couramment utilisées, qui sont en fait des combinaisons des portes ET, OU et NON :
- NAND (NON ET) : La sortie est l'inverse de la porte ET.
- NOR (NON OU) : La sortie est l'inverse de la porte OU.
- XOR (OU Exclusif) : La sortie est vraie (1) si les entrées sont différentes (une seule est vraie).
- XNOR (NON OU Exclusif) : La sortie est vraie (1) si les entrées sont identiques.
Ces portes, bien que dérivées, sont fondamentales pour la simplification et l'optimisation des circuits.
Importance de la table de vérité
La table de vérité de chaque porte logique est un outil essentiel pour comprendre son fonctionnement. Elle permet de prédire le comportement de la porte pour n'importe quelle combinaison d'entrées. En analysant les tables de vérité, on peut concevoir des circuits plus complexes en combinant plusieurs portes logiques. La table de vérité est utilisée pour :
- Simuler un circuit logique.
- Simplifier l'expression logique.
- Vérifier la conformité du design face à une spécification.
Ce qu'il faut retenir
- Les portes logiques sont les briques de base des circuits numériques.
- Les portes ET, OU et NON sont les portes fondamentales.
- Chaque porte logique a une table de vérité qui définit son comportement.
- La porte ET donne 1 en sortie seulement si TOUTES les entrées sont à 1.
- La porte OU donne 1 en sortie si AU MOINS UNE entrée est à 1.
- La porte NON inverse l'entrée.
- Les portes NAND, NOR, XOR et XNOR sont des combinaisons des portes fondamentales.
- Les portes logiques sont utilisées pour effectuer des opérations booléennes.
- La table de vérité permet d'identifier le fonctionnement de chaque porte logique.
FAQ
-
Quelle est la différence entre une porte ET et une porte OU ?
Une porte ET ne donne une sortie de 1 que si TOUTES ses entrées sont à 1. Une porte OU donne une sortie de 1 si AU MOINS UNE de ses entrées est à 1. -
À quoi sert la porte NON ?
La porte NON inverse le signal d'entrée. Si l'entrée est 1, la sortie est 0, et vice versa. Elle est utile pour créer des complémentations et des négations logiques. -
Comment puis-je combiner des portes logiques pour créer des circuits plus complexes ?
En connectant la sortie d'une porte logique à l'entrée d'une autre porte logique, vous pouvez créer des circuits plus complexes qui effectuent des opérations logiques plus sophistiquées. L'analyse des tables de vérité est cruciale pour comprendre et concevoir ces circuits combinatoires.
