Numérique et Sciences Informatiques > Représentation des Données : Types et Encodage > Types de Données de Base > Nombres flottants (norme IEEE 754)
Comprendre les Nombres Flottants IEEE 754
Explorez en détail la norme IEEE 754 pour les nombres flottants, essentielle en informatique. Apprenez comment les nombres réels sont représentés en binaire, les concepts de mantisse, d'exposant et de signe, et les implications de cette représentation pour la précision et les erreurs de calcul.
Introduction aux Nombres Flottants
Les nombres flottants sont une manière de représenter des nombres réels (avec des décimales) dans un ordinateur. Contrairement aux nombres entiers, ils peuvent représenter une plage beaucoup plus large de valeurs, y compris des nombres très grands et très petits. La norme la plus couramment utilisée pour représenter les nombres flottants est la norme IEEE 754.
La Norme IEEE 754 : Un Standard International
L'IEEE 754 est une norme technique pour la représentation des nombres flottants en binaire. Elle définit des formats de représentation, des règles d'arrondi et des opérations arithmétiques. Cette norme garantit une certaine cohérence entre les différents systèmes informatiques.
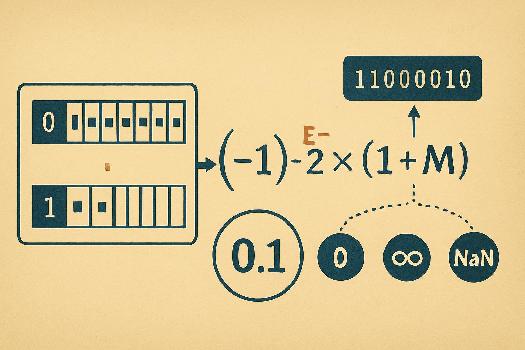
Structure d'un Nombre Flottant IEEE 754
Un nombre flottant IEEE 754 est composé de trois parties principales :
- Le Signe (S) : 1 bit qui indique si le nombre est positif (0) ou négatif (1).
- L'Exposant (E) : Un nombre entier utilisé pour pondérer la mantisse. L'exposant est biaisé, c'est-à-dire qu'une valeur constante lui est ajoutée pour pouvoir représenter des exposants positifs et négatifs sans utiliser de bit de signe supplémentaire.
- La Mantisse (M) : Aussi appelée significande, elle représente les chiffres significatifs du nombre. Elle est normalisée pour avoir la forme 1,xxxx, où xxxx sont les bits de fraction. Le '1,' initial est implicite (sauf dans certains cas spéciaux), ce qui permet de gagner un bit de précision.
Il existe principalement deux formats couramment utilisés :
- Simple Précision (32 bits) : 1 bit pour le signe, 8 bits pour l'exposant, et 23 bits pour la mantisse.
- Double Précision (64 bits) : 1 bit pour le signe, 11 bits pour l'exposant, et 52 bits pour la mantisse.
Calcul de la Valeur d'un Nombre Flottant
La valeur d'un nombre flottant peut être calculée en utilisant la formule suivante :
(-1)S * 2(E - Biais) * (1 + M)
Où :
Sest le bit de signe.Eest la valeur de l'exposant.Biaisest une valeur constante ajoutée à l'exposant (127 pour la simple précision et 1023 pour la double précision).Mest la valeur de la mantisse (la partie après la virgule).
Exemple :
Considérons un nombre flottant en simple précision : 0 10000000 10100000000000000000000
- Signe (S) = 0 (positif)
- Exposant (E) = 10000000 (binaire) = 128 (décimal)
- Mantisse (M) = 10100000000000000000000 (binaire) = 0.625 (décimal)
- Biais = 127
Valeur = (-1)0 * 2(128 - 127) * (1 + 0.625) = 1 * 21 * 1.625 = 3.25
Cas Spéciaux : Zéro, Infini et NaN
La norme IEEE 754 définit des représentations spéciales pour certains cas particuliers :
- Zéro : L'exposant et la mantisse sont tous les deux à zéro. Il existe un zéro positif (+0) et un zéro négatif (-0).
- Infini : L'exposant est rempli de 1 et la mantisse est à zéro. Il existe un infini positif (+∞) et un infini négatif (-∞).
- NaN (Not a Number) : L'exposant est rempli de 1 et la mantisse est différente de zéro. NaN est utilisé pour représenter des opérations non définies, comme la division de zéro par zéro.
Précision et Erreurs d'Arrondi
Les nombres flottants ont une précision limitée. En raison du nombre fini de bits utilisés pour représenter la mantisse, certains nombres réels ne peuvent pas être représentés exactement. Cela conduit à des erreurs d'arrondi. Par exemple, le nombre 0.1 ne peut pas être représenté exactement en binaire, ce qui peut entraîner des erreurs dans les calculs répétitifs. Il est important de comprendre ces limitations et d'utiliser des techniques appropriées pour minimiser les erreurs dans les applications qui nécessitent une grande précision.
Impact sur la Programmation
En programmation, il est crucial de comprendre comment les nombres flottants sont gérés. La comparaison directe de nombres flottants (avec ==) peut être problématique à cause des erreurs d'arrondi. Il est préférable d'utiliser une marge d'erreur (epsilon) pour vérifier si deux nombres flottants sont suffisamment proches l'un de l'autre. De plus, l'ordre des opérations peut affecter le résultat final en raison de la façon dont les erreurs d'arrondi s'accumulent.
Ce qu'il faut retenir
- La norme IEEE 754 est utilisée pour représenter les nombres flottants en binaire.
- Un nombre flottant est composé d'un bit de signe, d'un exposant et d'une mantisse.
- La valeur d'un nombre flottant est calculée en utilisant la formule :
(-1)S * 2(E - Biais) * (1 + M). - Des cas spéciaux existent pour zéro, infini et NaN.
- Les nombres flottants ont une précision limitée, ce qui conduit à des erreurs d'arrondi.
- Il est important de comprendre ces limitations en programmation et d'utiliser des techniques pour minimiser les erreurs.
FAQ
-
Pourquoi les nombres flottants ne sont-ils pas toujours précis ?
Les nombres flottants ont une précision limitée car ils utilisent un nombre fini de bits pour représenter un nombre potentiellement infini de décimales. Cela conduit à des erreurs d'arrondi. -
Qu'est-ce que le 'biais' dans l'exposant ?
Le biais est une valeur ajoutée à l'exposant pour permettre de représenter des exposants positifs et négatifs sans utiliser de bit de signe supplémentaire. Il vaut 127 pour la simple précision et 1023 pour la double précision. -
Comment comparer correctement deux nombres flottants en programmation ?
Au lieu d'utiliser l'égalité stricte (==), il est préférable d'utiliser une marge d'erreur (epsilon) pour vérifier si la différence entre les deux nombres est inférieure à cette marge. Exemple :abs(a - b) < epsilon.
