Conversion Binaire ↔ Hexadécimal : Guide Complet pour le Lycée

Introduction aux Systèmes Binaire et Hexadécimal

Le système binaire est un système de numération de base 2, utilisant uniquement les chiffres 0 et 1. Il est fondamental en informatique car les ordinateurs fonctionnent en interne avec des signaux électriques qui sont soit 'on' (1) soit 'off' (0). Le système hexadécimal, quant à lui, est un système de numération de base 16. Il utilise les chiffres de 0 à 9 et les lettres de A à F pour représenter les valeurs de 10 à 15. L'hexadécimal est souvent utilisé pour représenter des nombres binaires de manière plus compacte et lisible, facilitant ainsi le travail des programmeurs et des ingénieurs.

Conversion du Binaire vers l'Hexadécimal

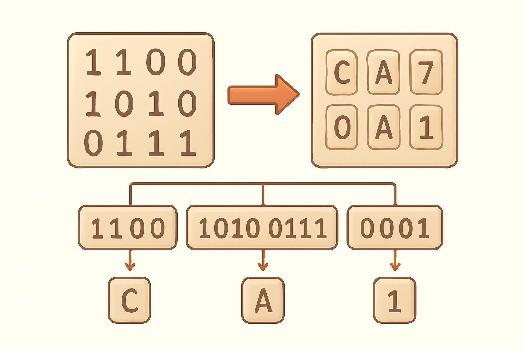
La conversion du binaire vers l'hexadécimal est un processus simple grâce à la relation directe entre les deux bases. Voici les étapes:

1. Regroupez les chiffres binaires par groupes de 4, en partant de la droite. Si le dernier groupe à gauche n'a pas 4 chiffres, ajoutez des zéros à gauche pour compléter le groupe.
2. Convertissez chaque groupe de 4 chiffres binaires en son équivalent hexadécimal. Utilisez la table de conversion suivante:

Binaire	Hexadécimal
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

1. Regroupement: 0001 1010 1101
2. Conversion: 0001 → 1, 1010 → A, 1101 → D

Conversion de l'Hexadécimal vers le Binaire

La conversion de l'hexadécimal vers le binaire est l'inverse du processus précédent. Voici les étapes:

1. Convertissez chaque chiffre hexadécimal en son équivalent binaire de 4 chiffres. Utilisez la même table de conversion que précédemment.
2. Concaténez les groupes binaires de 4 chiffres pour obtenir le nombre binaire final.

1. Conversion: 2 → 0010, B → 1011
2. Concaténation: 0010 1011

Pourquoi Utiliser l'Hexadécimal?

L'hexadécimal est particulièrement utile car il permet de représenter de grands nombres binaires de manière plus concise. Par exemple, un octet (8 bits) peut être représenté par seulement deux chiffres hexadécimaux. Ceci rend la lecture et l'écriture de données binaires beaucoup plus faciles pour les humains. De plus, l'hexadécimal est couramment utilisé pour représenter les couleurs en informatique (par exemple, #FF0000 pour le rouge) et les adresses mémoire.

Ce qu'il faut retenir

• Le binaire est en base 2 (0 et 1).
• L'hexadécimal est en base 16 (0-9 et A-F).
• Pour convertir du binaire à l'hexadécimal, groupez les bits par 4 et convertissez chaque groupe.
• Pour convertir de l'hexadécimal au binaire, convertissez chaque chiffre hexadécimal en un groupe de 4 bits.
• L'hexadécimal est plus compact et plus facile à lire que le binaire pour représenter des nombres importants.