La Machine de Turing : Un Modèle Fondamental de l'Informatique

Introduction à la Machine de Turing

La Machine de Turing, inventée par Alan Turing en 1936, est un modèle théorique de calcul. Imaginez-la comme un ordinateur très simple, mais capable d'effectuer n'importe quel calcul imaginable, à condition qu'on lui fournisse les bonnes instructions. Elle n'est pas un objet physique, mais un concept mathématique.

L'objectif de Turing était de définir rigoureusement la notion de calculabilité : qu'est-ce qu'une machine peut calculer ? La machine de Turing est devenue la pierre angulaire de la théorie de la calculabilité et a profondément influencé le développement de l'informatique.

Les Composants d'une Machine de Turing

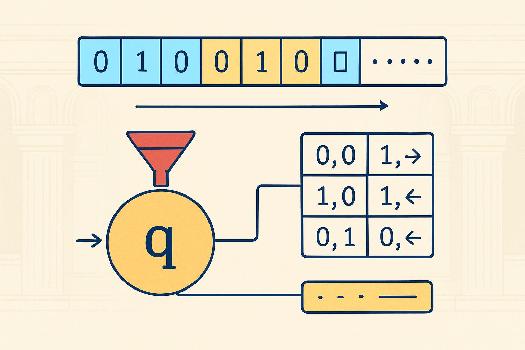
Une machine de Turing est constituée de plusieurs éléments clés :

1. Un ruban infini : Ce ruban est divisé en cellules, chacune pouvant contenir un symbole (par exemple, un '0', un '1', ou un symbole spécial indiquant une case vide). Le ruban est infini, ce qui signifie qu'il s'étend à l'infini dans les deux directions.
2. Une tête de lecture/écriture : Cette tête peut lire le symbole contenu dans la cellule courante du ruban, écrire un nouveau symbole dans cette cellule, et se déplacer d'une cellule vers la gauche ou vers la droite.
3. Un état : La machine se trouve à un moment donné dans un certain état. On peut imaginer l'état comme une configuration interne de la machine.
4. Une table de transition : C'est le 'programme' de la machine. Cette table définit ce que la machine doit faire en fonction de son état courant et du symbole qu'elle lit sur le ruban. Elle indique :
   • Quel symbole écrire sur le ruban.
   • Dans quelle direction déplacer la tête (gauche ou droite).
   • Quel sera le nouvel état de la machine.

Fonctionnement de la Machine de Turing

Voici comment une machine de Turing effectue un calcul :

1. Initialisation : Le ruban est initialisé avec les données d'entrée du calcul. Le reste du ruban est rempli de symboles 'vide'. La tête de lecture/écriture est positionnée sur la première cellule du ruban, et la machine est dans son état initial.
2. Exécution : La machine lit le symbole sous la tête de lecture/écriture et consulte sa table de transition pour déterminer l'action à effectuer. Elle écrit un nouveau symbole, déplace la tête, et change d'état, conformément à la table.
3. Répétition : L'étape 2 est répétée jusqu'à ce que la machine atteigne un état final, appelé état d'acceptation ou état de rejet. L'atteinte de cet état signifie que le calcul est terminé.

Si la machine atteint un état d'acceptation, cela signifie que le calcul a réussi. Si elle atteint un état de rejet, cela signifie que le calcul a échoué. Il est également possible que la machine ne s'arrête jamais, et continue à effectuer des opérations indéfiniment.

Exemple Simple : Machine de Turing pour Inverser une Chaîne de 0 et de 1

Imaginons une machine de Turing qui prend en entrée une chaîne de 0 et de 1, et qui l'inverse. Par exemple, si l'entrée est '101', la sortie sera '101' (car elle est déjà un palindrome). Si l'entrée est '110', la sortie sera '011'.

Voici une description simplifiée du fonctionnement possible :

1. Parcourir la chaîne : La machine parcourt la chaîne de gauche à droite, en mémorisant le premier symbole.
2. Retour au début : Elle revient ensuite au début de la chaîne.
3. Inversion : Elle écrit le symbole mémorisé à la fin de la chaîne (en ajoutant une case vide si nécessaire) et supprime le symbole initial.
4. Répétition : Elle répète ces étapes jusqu'à ce que toute la chaîne soit inversée.

La table de transition de cette machine serait plus complexe, mais c'est un exemple pour illustrer son fonctionnement.

Importance de la Machine de Turing

La machine de Turing est un concept fondamental pour plusieurs raisons :

• Universalité : Une machine de Turing universelle (MTU) est une machine de Turing qui peut simuler n'importe quelle autre machine de Turing. Cela signifie qu'elle peut exécuter n'importe quel algorithme, à condition qu'on lui fournisse la description de cet algorithme sous forme de table de transition. C'est le concept à la base des ordinateurs modernes.
• Calculabilité : La machine de Turing a permis de définir rigoureusement ce qui est calculable. Les problèmes qui peuvent être résolus par une machine de Turing sont dits 'calculables'.
• Limites du calcul : Elle a également permis de démontrer l'existence de problèmes 'indécidables', c'est-à-dire des problèmes pour lesquels il n'existe pas d'algorithme (ni de machine de Turing) capable de les résoudre dans tous les cas.

Ce qu'il faut retenir

• La machine de Turing est un modèle théorique de calcul inventé par Alan Turing.
• Elle se compose d'un ruban infini, d'une tête de lecture/écriture, d'un état, et d'une table de transition.
• Elle fonctionne en lisant un symbole sur le ruban, en effectuant une action (écriture, déplacement), et en changeant d'état, selon sa table de transition.
• Une machine de Turing universelle peut simuler n'importe quelle autre machine de Turing.
• La machine de Turing a permis de définir la notion de calculabilité et de démontrer l'existence de problèmes indécidables.