Numérique et Sciences Informatiques > Algorithmique : Tris et Recherche > Algorithmes de Tri Élémentaires > Tri par insertion

Le Tri par Insertion : Un Guide Complet

Découvrez le tri par insertion, un algorithme de tri simple et intuitif, parfait pour les petits ensembles de données. Apprenez son fonctionnement, son implémentation et son analyse de complexité.

Introduction au Tri par Insertion

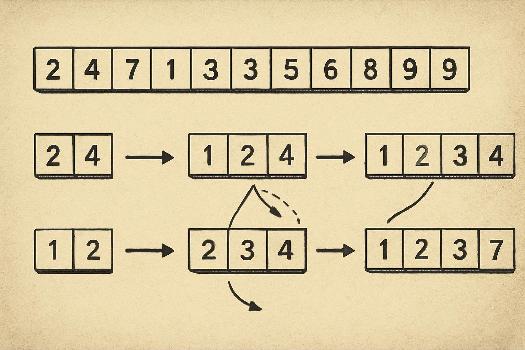
Le tri par insertion est un algorithme de tri simple qui fonctionne un peu comme la façon dont on trie des cartes à jouer dans sa main. L'idée est de parcourir le tableau (ou la liste) et d'insérer chaque élément à sa place dans la partie déjà triée du tableau. C'est un algorithme intuitif, facile à comprendre et à implémenter, particulièrement efficace pour les petits ensembles de données ou les données presque triées.

Principe de Fonctionnement

Le tri par insertion fonctionne en maintenant une sous-liste triée au début du tableau. Pour chaque nouvel élément non trié, on le compare aux éléments de la sous-liste triée, en le faisant reculer jusqu'à trouver sa position correcte, puis on l'insère à cet endroit. Voici les étapes détaillées :

  1. Initialisation : La première position du tableau est considérée comme une sous-liste triée de taille 1.
  2. Itération : On parcourt le reste du tableau, un élément à la fois. Pour chaque élément, on le compare avec les éléments de la sous-liste triée, de droite à gauche.
  3. Décalage : Si l'élément courant est plus petit que l'élément de la sous-liste triée, on décale l'élément de la sous-liste triée d'une position vers la droite.
  4. Insertion : On répète l'étape de décalage jusqu'à trouver la position correcte pour insérer l'élément courant. Une fois la position trouvée, on insère l'élément à cet endroit.
  5. Répétition : On répète les étapes 2 à 4 jusqu'à ce que tous les éléments du tableau aient été insérés dans la sous-liste triée.

Exemple Concret

Prenons le tableau suivant : [5, 2, 4, 6, 1, 3]. Illustrons le tri par insertion étape par étape :

  1. [5, 2, 4, 6, 1, 3] : La sous-liste triée est [5].
  2. [2, 5, 4, 6, 1, 3] : On insère 2 avant 5. La sous-liste triée est [2, 5].
  3. [2, 4, 5, 6, 1, 3] : On insère 4 entre 2 et 5. La sous-liste triée est [2, 4, 5].
  4. [2, 4, 5, 6, 1, 3] : 6 est déjà à sa place. La sous-liste triée est [2, 4, 5, 6].
  5. [1, 2, 4, 5, 6, 3] : On insère 1 au début. La sous-liste triée est [1, 2, 4, 5, 6].
  6. [1, 2, 3, 4, 5, 6] : On insère 3 entre 2 et 4. Le tableau est maintenant trié.

Implémentation en Python

Voici une implémentation simple du tri par insertion en Python : def tri_insertion(tableau): n = len(tableau) for i in range(1, n): cle = tableau[i] j = i - 1 while j >= 0 and tableau[j] > cle: tableau[j + 1] = tableau[j] j -= 1 tableau[j + 1] = cle return tableau # Exemple d'utilisation tableau = [5, 2, 4, 6, 1, 3] tableau_trie = tri_insertion(tableau) print(tableau_trie) # Output: [1, 2, 3, 4, 5, 6] Explication du code :

  • La boucle for i in range(1, n) parcourt le tableau à partir du deuxième élément (indice 1).
  • cle = tableau[i] stocke la valeur de l'élément à insérer.
  • La boucle while j >= 0 and tableau[j] > cle compare l'élément à insérer avec les éléments de la sous-liste triée.
  • tableau[j + 1] = tableau[j] décale l'élément de la sous-liste triée vers la droite.
  • tableau[j + 1] = cle insère l'élément à sa place correcte.

Complexité du Tri par Insertion

La complexité du tri par insertion varie en fonction du cas :

  • Cas le plus favorable : Le tableau est déjà trié. La complexité est de O(n), car on parcourt le tableau une seule fois.
  • Cas moyen et le plus défavorable : Le tableau est trié en ordre inverse ou est aléatoire. La complexité est de O(n²), car pour chaque élément, on doit potentiellement parcourir toute la sous-liste triée.
En termes d'utilisation de la mémoire, le tri par insertion est un algorithme en place, ce qui signifie qu'il ne nécessite pas de mémoire supplémentaire (complexité spatiale de O(1)).

Avantages et Inconvénients

Avantages :

  • Simple à comprendre et à implémenter.
  • Efficace pour les petits ensembles de données.
  • Efficace pour les données presque triées.
  • En place (ne nécessite pas de mémoire supplémentaire).
  • Stable (préserve l'ordre relatif des éléments égaux).
Inconvénients :
  • Inefficace pour les grands ensembles de données (complexité quadratique).

Quand Utiliser le Tri par Insertion ?

Le tri par insertion est particulièrement adapté dans les situations suivantes :

  • Lorsque le tableau à trier est petit (moins de quelques dizaines d'éléments).
  • Lorsque les données sont presque triées.
  • Lorsque la simplicité de l'implémentation est plus importante que la performance.
Pour les grands ensembles de données, d'autres algorithmes de tri plus performants, tels que le tri fusion (Merge Sort) ou le tri rapide (Quick Sort), sont généralement préférés.

Ce qu'il faut retenir

  • Le tri par insertion est un algorithme de tri simple et intuitif qui trie un tableau en insérant chaque élément à sa place dans la partie déjà triée du tableau.
  • Il fonctionne en maintenant une sous-liste triée au début du tableau et en insérant les éléments non triés à leur position correcte dans cette sous-liste.
  • La complexité du tri par insertion est de O(n²) dans le cas moyen et le pire, mais de O(n) dans le cas le plus favorable (tableau déjà trié).
  • Il est efficace pour les petits ensembles de données ou les données presque triées.
  • C'est un algorithme en place, ce qui signifie qu'il ne nécessite pas de mémoire supplémentaire.
  • Le tri par insertion est stable, préservant l'ordre relatif des éléments égaux.

← La Recherche Linéaire : Une Introduction Simple Le Tri par Sélection : Une Méthode de Tri Simple et Efficace →

FAQ

  • Quelle est la différence entre le tri par insertion et le tri par sélection ?

    Le tri par insertion insère chaque élément à sa place dans une sous-liste triée, tandis que le tri par sélection sélectionne l'élément minimum du tableau et l'échange avec l'élément à la position courante.
  • Le tri par insertion est-il un algorithme de tri stable ?

    Oui, le tri par insertion est un algorithme de tri stable. Il préserve l'ordre relatif des éléments égaux.
  • Quand est-il préférable d'utiliser le tri par insertion plutôt que le tri rapide ?

    Le tri par insertion est préférable lorsque le tableau est petit ou presque trié. Le tri rapide est généralement plus rapide pour les grands ensembles de données aléatoires.