Évaluation d'Expressions Arithmétiques

Notation Infixe, Préfixe et Postfixe (RPN)

Avant d'aborder l'évaluation, il est important de comprendre les différentes notations utilisées pour représenter les expressions arithmétiques. * Notation Infixe : C'est la notation la plus courante, où l'opérateur est placé entre les opérandes (ex: 2 + 3). * Notation Préfixe (Polonaise) : L'opérateur est placé avant les opérandes (ex: + 2 3). * Notation Postfixe (Polonaise Inverse - RPN) : L'opérateur est placé après les opérandes (ex: 2 3 +). La notation RPN est particulièrement intéressante pour l'évaluation avec des piles.

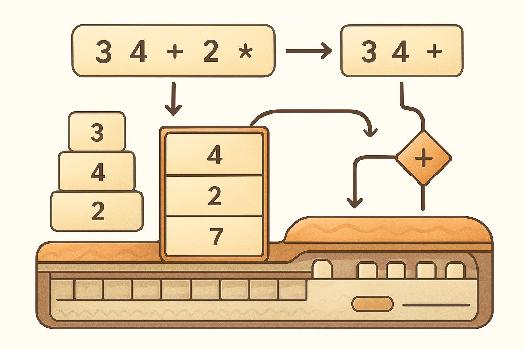
Algorithme d'Évaluation RPN avec une Pile

L'algorithme pour évaluer une expression en notation RPN utilise une pile de la manière suivante : 1. Parcourir l'expression RPN de gauche à droite. 2. Si l'élément courant est un nombre, l'empiler dans la pile. 3. Si l'élément courant est un opérateur : * Dépiler les deux nombres du sommet de la pile (opérande2, opérande1). * Appliquer l'opérateur aux deux opérandes (opérande1 opérateur opérande2). * Empiler le résultat dans la pile. 4. À la fin du parcours, le résultat de l'expression se trouve au sommet de la pile. Exemple : Évaluer l'expression RPN `2 3 + 5 *` 1. Empiler 2. 2. Empiler 3. 3. Rencontre l'opérateur '+'. Dépiler 3 et 2. Calculer 2 + 3 = 5. Empiler 5. 4. Empiler 5. 5. Rencontre l'opérateur '*'. Dépiler 5 et 5. Calculer 5 * 5 = 25. Empiler 25. 6. La pile contient 25, qui est le résultat de l'expression.

Implémentation en Code (Exemple Python)

Voici un exemple d'implémentation en Python pour évaluer une expression RPN : python def evaluer_rpn(expression): pile = [] operateurs = ['+', '-', '*', '/'] tokens = expression.split() for token in tokens: if token in operateurs: if len(pile) < 2: raise ValueError("Expression RPN invalide") op2 = pile.pop() op1 = pile.pop() if token == '+': resultat = op1 + op2 elif token == '-': resultat = op1 - op2 elif token == '*': resultat = op1 * op2 elif token == '/': if op2 == 0: raise ZeroDivisionError("Division par zéro") resultat = op1 / op2 pile.append(resultat) else: try: pile.append(float(token)) except ValueError: raise ValueError("Token invalide : " + token) if len(pile) != 1: raise ValueError("Expression RPN invalide") return pile[0] # Exemple d'utilisation expression = "2 3 + 5 *" resultat = evaluer_rpn(expression) print(f"Le résultat de l'expression {expression} est : {resultat}") # Affiche: Le résultat de l'expression 2 3 + 5 * est : 25.0 Ce code montre comment utiliser une pile pour traiter les opérandes et les opérateurs dans l'ordre correct.

Avantages de l'Évaluation RPN avec des Piles

L'utilisation d'une pile pour évaluer des expressions RPN présente plusieurs avantages : * Simplicité : L'algorithme est simple à comprendre et à implémenter. * Efficacité : L'évaluation est rapide car elle ne nécessite pas de gérer la précédence des opérateurs avec des parenthèses. * Adaptabilité : L'algorithme peut être facilement étendu pour supporter d'autres opérateurs et fonctions.

Ce qu'il faut retenir

• Notation RPN : L'opérateur suit les opérandes.
• Évaluation RPN : Utilisation d'une pile pour stocker les opérandes et appliquer les opérateurs.
• Algorithme : Parcourir l'expression, empiler les nombres, dépiler et opérer lors de la rencontre d'un opérateur.
• Avantages : Simplicité, efficacité, adaptabilité.