Numérique et Sciences Informatiques > Architecture des Ordinateurs > Systèmes d'Exploitation (OS) > Gestion des fichiers
Représentation des Nombres en Binaire et Hexadécimal
Comprendre comment les nombres sont représentés en binaire et hexadécimal, les bases fondamentales de l'architecture des ordinateurs.
Introduction au Système Binaire
Le système binaire est un système de numération en base 2. Contrairement au système décimal (base 10) que nous utilisons quotidiennement, le système binaire n'utilise que deux chiffres : 0 et 1. Ces chiffres sont appelés bits (binary digits).
Les ordinateurs utilisent le système binaire car il est simple de représenter deux états physiques différents (par exemple, présence ou absence de tension électrique) avec 0 et 1.
Conversion Décimal vers Binaire
Pour convertir un nombre décimal en binaire, on utilise la méthode des divisions successives par 2. On divise le nombre décimal par 2, on note le quotient et le reste. On répète l'opération avec le quotient jusqu'à obtenir un quotient de 0. Les restes, lus de bas en haut, forment le nombre binaire.
Exemple: Convertissons le nombre décimal 25 en binaire.
| Division | Quotient | Reste |
|---|---|---|
| 25 / 2 | 12 | 1 |
| 12 / 2 | 6 | 0 |
| 6 / 2 | 3 | 0 |
| 3 / 2 | 1 | 1 |
| 1 / 2 | 0 | 1 |
Le nombre binaire correspondant à 25 est donc 11001.
Conversion Binaire vers Décimal
Pour convertir un nombre binaire en décimal, on multiplie chaque bit par 2 élevé à la puissance de sa position (en commençant par la position 0 à partir de la droite), puis on additionne les résultats.
Exemple: Convertissons le nombre binaire 10110 en décimal.
10110 = (1 * 24) + (0 * 23) + (1 * 22) + (1 * 21) + (0 * 20) = 16 + 0 + 4 + 2 + 0 = 22.
Introduction au Système Hexadécimal
Le système hexadécimal est un système de numération en base 16. Il utilise 16 symboles : les chiffres de 0 à 9, et les lettres de A à F, où A représente 10, B représente 11, C représente 12, D représente 13, E représente 14, et F représente 15.
Le système hexadécimal est souvent utilisé pour représenter des nombres binaires de manière plus compacte et lisible. Chaque chiffre hexadécimal correspond à 4 bits.
Conversion Binaire vers Hexadécimal
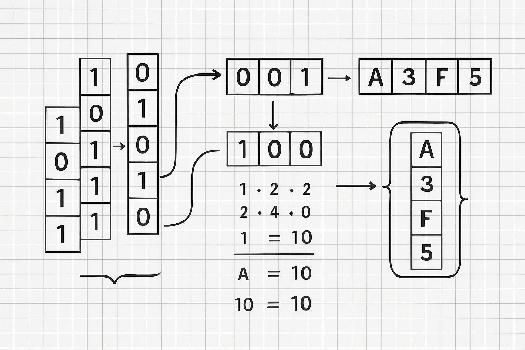
Pour convertir un nombre binaire en hexadécimal, on regroupe les bits par groupes de 4, en commençant par la droite. Si le dernier groupe n'a pas 4 bits, on ajoute des zéros à gauche. Ensuite, on convertit chaque groupe de 4 bits en son équivalent hexadécimal.
Exemple: Convertissons le nombre binaire 1101011010 en hexadécimal.
On le regroupe en 11 0101 1010. On ajoute un zéro à gauche du premier groupe: 0011 0101 1010.
0011 = 3, 0101 = 5, 1010 = A (10 en décimal). Donc, 1101011010 en binaire est 35A en hexadécimal.
Conversion Hexadécimal vers Binaire
Pour convertir un nombre hexadécimal en binaire, on remplace chaque chiffre hexadécimal par son équivalent en 4 bits.
Exemple: Convertissons le nombre hexadécimal 2B en binaire.
2 = 0010, B = 1011. Donc, 2B en hexadécimal est 00101011 en binaire.
Conversion Décimal vers Hexadécimal
Pour convertir un nombre décimal en hexadécimal, on utilise la méthode des divisions successives par 16. On divise le nombre décimal par 16, on note le quotient et le reste. Si le reste est supérieur à 9, on le remplace par sa lettre correspondante (A à F). On répète l'opération avec le quotient jusqu'à obtenir un quotient de 0. Les restes, lus de bas en haut, forment le nombre hexadécimal.
Exemple: Convertissons le nombre décimal 42 en hexadécimal.
| Division | Quotient | Reste |
|---|---|---|
| 42 / 16 | 2 | 10 (A) |
| 2 / 16 | 0 | 2 |
Le nombre hexadécimal correspondant à 42 est donc 2A.
Conversion Hexadécimal vers Décimal
Pour convertir un nombre hexadécimal en décimal, on multiplie chaque chiffre hexadécimal par 16 élevé à la puissance de sa position (en commençant par la position 0 à partir de la droite), puis on additionne les résultats. N'oubliez pas que A=10, B=11, C=12, D=13, E=14, et F=15.
Exemple: Convertissons le nombre hexadécimal 1A en décimal.
1A = (1 * 161) + (10 * 160) = 16 + 10 = 26.
Ce qu'il faut retenir
- Le système binaire utilise uniquement les chiffres 0 et 1 (bits).
- Le système hexadécimal utilise les chiffres 0-9 et les lettres A-F.
- La conversion décimal vers binaire se fait par divisions successives par 2.
- La conversion binaire vers décimal se fait en multipliant chaque bit par 2 puissance sa position.
- La conversion décimal vers hexadécimal se fait par divisions successives par 16.
- La conversion hexadécimal vers décimal se fait en multipliant chaque chiffre par 16 puissance sa position.
- La conversion binaire vers hexadécimal se fait en groupant les bits par 4.
- La conversion hexadécimal vers binaire se fait en remplaçant chaque chiffre par son équivalent en 4 bits.
FAQ
-
Pourquoi les ordinateurs utilisent-ils le système binaire?
Parce qu'il est simple de représenter deux états physiques différents (présence ou absence de tension électrique) avec 0 et 1. -
Quelle est la relation entre le binaire et l'hexadécimal?
Chaque chiffre hexadécimal correspond à 4 bits, ce qui facilite la conversion entre les deux systèmes. -
Comment gérer les restes supérieurs à 9 lors de la conversion décimal vers hexadécimal?
On remplace les restes 10 à 15 par les lettres A à F respectivement.
