Introduction aux Arbres Binaires : Définition et Terminologie

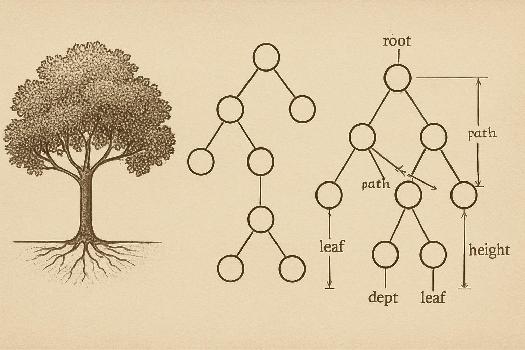
Qu'est-ce qu'un Arbre Binaire ?

Un arbre binaire est une structure de données hiérarchique où chaque nœud a au plus deux enfants, appelés enfant gauche et enfant droit. C'est une structure de données fondamentale en informatique, utilisée pour représenter des données de manière organisée et efficace.

Contrairement aux arbres génériques, la limitation à deux enfants rend les arbres binaires particulièrement adaptés à certains algorithmes et applications, comme les arbres de recherche binaire ou les arbres de Huffman.

Exemple simple : Imaginez un arbre généalogique simplifié. Chaque personne (nœud) a au plus deux enfants (enfant gauche et enfant droit). Certaines personnes peuvent n'avoir qu'un enfant, ou aucun.

Terminologie Essentielle

• Nœud : Un élément de l'arbre. Il contient une valeur et des pointeurs vers ses enfants.
• Racine : Le nœud le plus haut de l'arbre. C'est le seul nœud qui n'a pas de parent.
• Enfant : Un nœud directement connecté à un autre nœud lorsqu'on s'éloigne de la racine.
• Parent : Le nœud directement au-dessus d'un autre nœud lorsqu'on se rapproche de la racine.
• Feuille : Un nœud qui n'a pas d'enfants.
• Arête : La connexion entre un nœud parent et un nœud enfant.
• Chemin : Une séquence de nœuds et d'arêtes reliant un nœud à un descendant.
• Profondeur d'un nœud : Le nombre d'arêtes entre la racine et ce nœud. La profondeur de la racine est 0.
• Hauteur d'un arbre : La profondeur maximale de n'importe quel nœud de l'arbre. C'est aussi la longueur du chemin le plus long de la racine à une feuille.
• Sous-arbre gauche : L'arbre binaire dont la racine est l'enfant gauche d'un nœud.
• Sous-arbre droit : L'arbre binaire dont la racine est l'enfant droit d'un nœud.

Exemple illustratif : Considérons l'arbre binaire suivant (représentation textuelle simplifiée) :

        A
       / \
      B   C
     / \
    D   E
  

• A est la racine.
• B et C sont les enfants de A. A est le parent de B et C.
• D et E sont les enfants de B.
• C, D et E sont des feuilles.
• La profondeur de D est 2.
• La hauteur de l'arbre est 2.

Types d'Arbres Binaires

Il existe plusieurs types d'arbres binaires, chacun ayant des propriétés spécifiques:

• Arbre binaire complet: Tous les niveaux sont complètement remplis, sauf éventuellement le dernier niveau, qui est rempli de gauche à droite.
• Arbre binaire parfait: Tous les niveaux sont complètement remplis. Tous les nœuds non-feuilles ont deux enfants, et toutes les feuilles sont à la même profondeur.
• Arbre binaire dégénéré (ou arbre binaire filiforme): Chaque nœud a un seul enfant. L'arbre ressemble à une liste chaînée.
• Arbre binaire équilibré: La différence de hauteur entre les sous-arbres gauche et droit de chaque nœud est limitée. Cela garantit une performance optimale pour certaines opérations, comme la recherche. Des exemples d'arbres binaires équilibrés incluent les arbres AVL et les arbres rouge-noir.

Comprendre ces types est crucial pour choisir la structure d'arbre binaire la plus appropriée pour une application donnée.

Ce qu'il faut retenir

• Un arbre binaire est une structure de données hiérarchique avec un maximum de deux enfants par nœud.
• La terminologie de base inclut : nœud, racine, enfant, parent, feuille, arête, chemin, profondeur et hauteur.
• Il existe différents types d'arbres binaires, tels que les arbres complets, parfaits, dégénérés et équilibrés.
• Le choix du type d'arbre binaire dépend de l'application et des performances souhaitées.