Tri Rapide (Quicksort) : Comprendre et Implémenter

Introduction au Tri Rapide

Le tri rapide (Quicksort) est un algorithme de tri basé sur le principe 'diviser pour régner'. Il est reconnu pour son efficacité en moyenne, ce qui en fait un choix populaire dans de nombreuses applications. L'idée principale est de partitionner le tableau en deux sous-tableaux autour d'un élément pivot, de telle sorte que tous les éléments inférieurs au pivot soient placés avant lui, et tous les éléments supérieurs soient placés après lui. Ensuite, les sous-tableaux sont triés récursivement.

Principe de Partitionnement

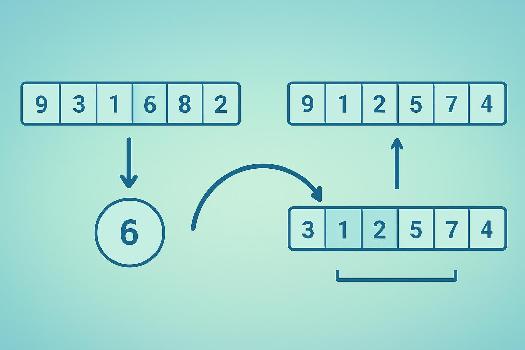
Le cœur du tri rapide est le processus de partitionnement. Il se déroule comme suit:

1. Choisir un pivot: Sélectionnez un élément du tableau comme pivot. Le choix du pivot peut affecter significativement la performance de l'algorithme. Des stratégies courantes incluent choisir le premier élément, le dernier élément, ou un élément aléatoire.
2. Réorganiser le tableau: Parcourez le tableau et comparez chaque élément au pivot. Les éléments inférieurs au pivot sont déplacés vers la gauche, et les éléments supérieurs sont déplacés vers la droite.
3. Position finale du pivot: Une fois le partitionnement terminé, le pivot est à sa position finale dans le tableau trié.

Algorithme Récursif

Après le partitionnement, deux sous-tableaux sont créés : un contenant les éléments inférieurs au pivot, et l'autre contenant les éléments supérieurs au pivot. Le tri rapide est ensuite appliqué récursivement à ces deux sous-tableaux. Cette récursion se poursuit jusqu'à ce que les sous-tableaux aient une taille de 0 ou 1, auquel cas ils sont trivialement triés.

Exemple d'Implémentation en Python

Voici un exemple d'implémentation du tri rapide en Python :

def quicksort(tableau):
    if len(tableau) <= 1:
        return tableau
    pivot = tableau[len(tableau) // 2]
    gauche = [x for x in tableau if x < pivot]
    milieu = [x for x in tableau if x == pivot]
    droite = [x for x in tableau if x > pivot]
    return quicksort(gauche) + milieu + quicksort(droite)

tableau = [7, 2, 1, 6, 8, 5, 3, 4]
tableau_trie = quicksort(tableau)
print(tableau_trie)  # Affiche [1, 2, 3, 4, 5, 6, 7, 8]

Analyse de Complexité

La complexité du tri rapide dépend du choix du pivot.

• Meilleur cas et cas moyen: O(n log n). Cela se produit lorsque le pivot divise le tableau en deux parties à peu près égales à chaque étape.
• Pire cas: O(n^2). Cela se produit lorsque le pivot est toujours le plus petit ou le plus grand élément du tableau. Par exemple, si le tableau est déjà trié et que le pivot est toujours le premier élément.

Stratégies d'Optimisation

Plusieurs techniques peuvent être utilisées pour optimiser le tri rapide :

• Choix du pivot: Choisir un pivot aléatoire ou la médiane de trois éléments peut réduire la probabilité du pire cas.
• Tri par insertion pour les petits tableaux: Pour les petits sous-tableaux, le tri par insertion peut être plus efficace que le tri rapide. On peut donc utiliser le tri par insertion lorsque la taille du sous-tableau est inférieure à un certain seuil.
• Optimisation de la récursion terminale (tail recursion optimization): Dans certains langages, la récursion terminale peut être optimisée pour éviter le débordement de pile.

Ce qu'il faut retenir

• Le tri rapide est un algorithme de tri basé sur le principe 'diviser pour régner'.
• Il partitionne le tableau autour d'un pivot et trie récursivement les sous-tableaux.
• Sa complexité est de O(n log n) en moyenne et O(n^2) dans le pire cas.
• Le choix du pivot est crucial pour la performance.
• Des optimisations existent pour améliorer son efficacité, comme le choix d'un pivot aléatoire et l'utilisation du tri par insertion pour les petits tableaux.