Numérique et Sciences Informatiques > Numération et Bases > Systèmes de Numération > Base binaire

Comprendre la Base Binaire

Découvrez les fondements de la base binaire, un système de numération essentiel en informatique, utilisé pour représenter toutes les informations dans les ordinateurs. Ce guide vous expliquera comment convertir entre le système décimal et binaire, avec des exemples clairs et des applications pratiques.

Qu'est-ce que la base binaire ?

La base binaire est un système de numération qui utilise seulement deux chiffres : 0 et 1. Contrairement au système décimal (base 10) que nous utilisons quotidiennement, qui utilise dix chiffres (0 à 9), le système binaire est fondamental en informatique car il représente les deux états possibles d'un circuit électronique : ouvert (0) ou fermé (1). Tous les nombres, les textes, les images et les instructions que votre ordinateur traite sont convertis en séquences de 0 et de 1.

Position et Valeur des Chiffres Binaires

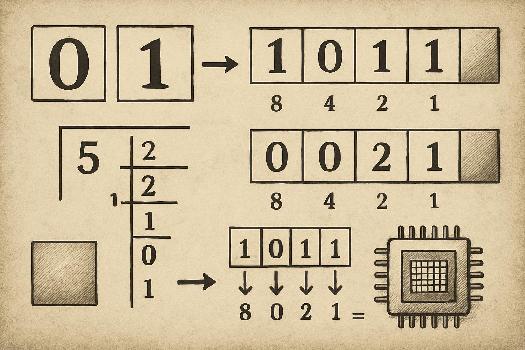
Dans le système binaire, chaque position d'un chiffre a une valeur qui est une puissance de 2. De droite à gauche, les positions représentent 20 (1), 21 (2), 22 (4), 23 (8), 24 (16), et ainsi de suite. Par exemple, dans le nombre binaire 1011 :

  • Le chiffre le plus à droite (1) représente 1 x 20 = 1
  • Le chiffre suivant (1) représente 1 x 21 = 2
  • Le chiffre suivant (0) représente 0 x 22 = 0
  • Le chiffre le plus à gauche (1) représente 1 x 23 = 8
Donc, le nombre binaire 1011 équivaut à 8 + 0 + 2 + 1 = 11 en base 10.

Conversion Décimal vers Binaire

Pour convertir un nombre décimal en binaire, on utilise la méthode des divisions successives par 2. Voici les étapes :

  1. Divisez le nombre décimal par 2.
  2. Notez le quotient et le reste (qui sera soit 0, soit 1).
  3. Divisez le quotient obtenu par 2 et notez à nouveau le quotient et le reste.
  4. Répétez l'étape 3 jusqu'à ce que le quotient soit égal à 0.
  5. Lisez les restes de bas en haut (du dernier reste au premier) pour obtenir le nombre binaire.
Exemple : Convertissons le nombre décimal 25 en binaire :
  • 25 ÷ 2 = 12 (reste 1)
  • 12 ÷ 2 = 6 (reste 0)
  • 6 ÷ 2 = 3 (reste 0)
  • 3 ÷ 2 = 1 (reste 1)
  • 1 ÷ 2 = 0 (reste 1)
En lisant les restes de bas en haut, on obtient 11001. Donc, 25 en base 10 est égal à 11001 en base 2.

Conversion Binaire vers Décimal

Pour convertir un nombre binaire en décimal, on multiplie chaque chiffre binaire par la puissance de 2 correspondante à sa position (en partant de 0 pour le chiffre le plus à droite) et on additionne les résultats.
Exemple : Convertissons le nombre binaire 101101 en décimal :

  • 1 x 25 = 1 x 32 = 32
  • 0 x 24 = 0 x 16 = 0
  • 1 x 23 = 1 x 8 = 8
  • 1 x 22 = 1 x 4 = 4
  • 0 x 21 = 0 x 2 = 0
  • 1 x 20 = 1 x 1 = 1
En additionnant les résultats, on obtient 32 + 0 + 8 + 4 + 0 + 1 = 45. Donc, 101101 en base 2 est égal à 45 en base 10.

Importance de la base binaire en informatique

La base binaire est au coeur de l'informatique moderne. Les ordinateurs utilisent des transistors qui peuvent être dans deux états: passant (1) ou bloquant (0). Ces états correspondent directement aux chiffres binaires. La base binaire permet de représenter:

  • Des nombres entiers et réels
  • Des caractères (via des tables de codage comme ASCII ou UTF-8)
  • Des images (chaque pixel est représenté par une combinaison de bits)
  • Des instructions de programmes (le code machine est une suite d'instructions en binaire)
Sans la base binaire, le fonctionnement des ordinateurs serait impossible. C'est pourquoi sa compréhension est cruciale pour tout étudiant en informatique.

Ce qu'il faut retenir

  • La base binaire utilise seulement deux chiffres : 0 et 1.
  • Chaque position dans un nombre binaire représente une puissance de 2.
  • La conversion décimal vers binaire se fait par divisions successives par 2.
  • La conversion binaire vers décimal se fait en multipliant chaque chiffre par sa puissance de 2 et en additionnant les résultats.
  • Le binaire est fondamental en informatique pour représenter les données et les instructions.

← Base Décimale : Représentation des Entiers Relatifs Conversion Binaire ↔ Hexadécimal : Guide Complet pour le Lycée →

FAQ

  • Pourquoi les ordinateurs utilisent-ils la base binaire ?

    Les ordinateurs utilisent la base binaire car les circuits électroniques sont plus simples à concevoir et à fabriquer avec seulement deux états (0 et 1). Cela permet de représenter et de traiter l'information de manière efficace.
  • Est-ce que tous les types de données peuvent être représentés en binaire ?

    Oui, tous les types de données (nombres, textes, images, vidéos, etc.) peuvent être représentés en binaire. Des conventions de codage spécifiques sont utilisées pour traduire chaque type de données en séquences de 0 et de 1.