Numérique et Sciences Informatiques > Algorithmique : Tris et Recherche > Algorithmes de Recherche > Recherche binaire (condition d'application)

La Recherche Binaire et ses Conditions d'Application

Découvrez les conditions essentielles pour appliquer efficacement l'algorithme de recherche binaire. Comprenez pourquoi le tri est crucial et explorez des exemples concrets pour le lycée.

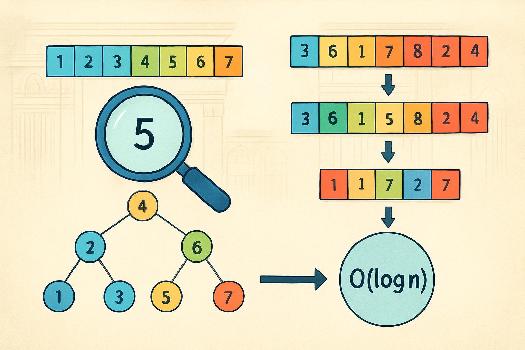
Introduction à la Recherche Binaire

La recherche binaire est un algorithme de recherche efficace qui permet de trouver un élément spécifique dans une liste triée. Contrairement à la recherche linéaire qui examine chaque élément un par un, la recherche binaire divise la liste en deux à chaque étape. Cela la rend beaucoup plus rapide pour les grandes listes. Imaginez chercher un mot dans un dictionnaire : vous ne commencez pas à la première page, vous ouvrez plutôt le dictionnaire au milieu et ajustez votre recherche en fonction de la lettre que vous voyez.

La Condition Essentielle : Le Tri

La condition fondamentale pour pouvoir appliquer la recherche binaire est que la liste dans laquelle on cherche soit triée. Si la liste n'est pas triée, l'algorithme de recherche binaire ne fonctionnera pas correctement et pourrait donner un résultat incorrect, voire planter.

Pourquoi le tri est-il si important ?

La recherche binaire repose sur le principe de diviser l'intervalle de recherche en deux parties. Si la liste n'est pas triée, il n'y a aucune garantie que l'élément recherché se trouve dans la moitié attendue. L'algorithme pourrait alors éliminer la partie de la liste qui contient l'élément recherché, ce qui conduirait à un échec.

Illustration avec un Exemple

Considérons une liste triée d'entiers : [2, 5, 7, 10, 13, 17, 20]. Nous voulons rechercher l'élément 13.

Étapes de la recherche binaire :

  1. On commence par le milieu de la liste : 10.
  2. 13 est supérieur à 10, donc on élimine la première moitié de la liste.
  3. On considère la deuxième moitié : [13, 17, 20].
  4. On prend le milieu : 17.
  5. 13 est inférieur à 17, donc on élimine la deuxième moitié de cette sous-liste.
  6. Il ne reste que [13].
  7. On a trouvé l'élément 13.
Si la liste n'était pas triée (par exemple : [5, 2, 17, 10, 20, 13, 7]), la recherche binaire ne donnerait pas un résultat correct. En effet, si l'on commençait par le milieu (10), on éliminerait la mauvaise portion de la liste.

Conséquences d'une Liste Non Triée

Si vous essayez d'appliquer la recherche binaire sur une liste non triée, voici ce qui pourrait se passer :

  • Résultat Incorrect : L'algorithme pourrait retourner un index incorrect, indiquant que l'élément est présent alors qu'il ne l'est pas, ou inversement.
  • Boucle Infinie : Dans certains cas, l'algorithme pourrait entrer dans une boucle infinie, car les conditions de fin de recherche ne seraient jamais atteintes.
  • Erreur d'exécution : L'algorithme pourrait tenter d'accéder à un index hors des limites de la liste, ce qui provoquerait une erreur.
Il est donc impératif de vérifier que la liste est triée avant d'utiliser la recherche binaire.

Comment S'assurer que la Liste est Triée?

Avant d'appliquer la recherche binaire, vous devez vous assurer que la liste est correctement triée. Voici quelques méthodes :

  • Vérification Manuelle : Pour les petites listes, vous pouvez simplement parcourir la liste et vérifier que chaque élément est bien placé par rapport à son voisin.
  • Utilisation d'Algorithmes de Tri : Pour les listes plus importantes, utilisez un algorithme de tri comme le tri par insertion, le tri par fusion ou le tri rapide (Quicksort) pour trier la liste avant d'effectuer la recherche binaire.
  • Bibliothèques : La plupart des langages de programmation offrent des fonctions de tri intégrées (par exemple, sorted() en Python) que vous pouvez utiliser pour trier la liste facilement.

Complexité de la Recherche Binaire

La recherche binaire est très efficace. Sa complexité temporelle est de O(log n), où n est le nombre d'éléments dans la liste. Cela signifie que le nombre d'opérations nécessaires pour trouver un élément augmente de manière logarithmique avec la taille de la liste. En comparaison, la recherche linéaire a une complexité de O(n), ce qui signifie que le nombre d'opérations augmente linéairement avec la taille de la liste.

Par exemple, si vous avez une liste de 1024 éléments, la recherche binaire ne nécessitera qu'environ 10 opérations pour trouver un élément (log₂1024 = 10), tandis que la recherche linéaire pourrait nécessiter jusqu'à 1024 opérations dans le pire des cas.

Ce qu'il faut retenir

  • La recherche binaire est un algorithme de recherche efficace pour les listes triées.
  • La condition principale pour son application est que la liste soit triée, sinon le résultat sera erroné.
  • Si la liste n'est pas triée, il faut la trier en utilisant un algorithme de tri avant d'appliquer la recherche binaire.
  • La complexité temporelle de la recherche binaire est de O(log n), ce qui la rend plus rapide que la recherche linéaire pour les grandes listes.
  • Pour les petites listes, on peut vérifier manuellement le tri, sinon on utilise un algorithme de tri ou une fonction de tri intégrée au langage de programmation.

← Implémentation du Tri par Sélection en Python La Recherche Linéaire : Une Introduction Simple →

FAQ

  • Que se passe-t-il si j'utilise la recherche binaire sur une liste non triée ?

    L'algorithme de recherche binaire ne fonctionnera pas correctement et pourrait donner un résultat incorrect, entrer dans une boucle infinie ou provoquer une erreur d'exécution.
  • Comment puis-je trier une liste en Python ?

    Vous pouvez utiliser la fonction sorted() pour créer une nouvelle liste triée à partir de la liste originale, ou la méthode .sort() pour trier la liste originale en place. Par exemple : ma_liste = [3, 1, 4, 1, 5, 9, 2, 6]; ma_liste_triee = sorted(ma_liste).
  • Pourquoi la recherche binaire est-elle plus rapide que la recherche linéaire pour les grandes listes ?

    La recherche binaire divise la liste en deux à chaque étape, ce qui réduit considérablement le nombre d'éléments à examiner. Sa complexité temporelle est de O(log n), tandis que celle de la recherche linéaire est de O(n). Cela signifie que le temps d'exécution de la recherche binaire augmente beaucoup plus lentement avec la taille de la liste que celui de la recherche linéaire.